Enrutamiento cuántico con teleportación

Por Ryan LaRose

Este post ha sido patrocinado por Tabor Electronics. Para mantenerte al día con los productos y aplicaciones de Tabor, únete a su comunidad en LinkedIn y suscríbete a su newsletter.

Autores: Dhruv Devulapalli, Eddie Schoute, Aniruddha Bapat, Andrew M. Childs, Alexey V. Gorshkov

arXiv: https://arxiv.org/abs/2204.04185

Contexto y motivación

Cuando escribimos circuitos cuánticos en papel o en software, es conveniente asumir que cualquier par de qubits están conectados. Es conveniente tanto para (i) alcanzar un nivel de abstracción – a veces no queremos pensar sobre detalles de hardware a bajo nivel cuando pensamos en algoritmos – como para (ii) porque es en cierta manera verdad – incluso si no hay una arista directa entre dos qubits, mientras haya algún camino conexo, los qubits pueden interactuar. Esto se muestra en la figura a continuación.

En el panel de la izquierda, la figura muestra un procesador superconductor de cinco qubits de IBMQ y en el panel de la derecha, se destacan las conexiones entre los qubits. Los qubits Q0 y Q1 están directamente conectados, pero los qubits Q0 y Q3 no lo están. Sin embargo, hay un camino conexo entre el qubit Q0 y el Q3, es decir, el camino Q0 – Q2 – Q3. Dado que este camino conexo existe, se pueden aplicar operaciones de dos qubits entre los qubits Q0 y Q3.

¿Cómo es esto posible? Intercambiar dos qubits es una operación unitaria – en efecto, es una operación autoinversa – y por tanto, una operación cuántica permitida. Además, se puede presuponer que es una operación disponible en un ordenador cuántico. De hecho, podemos componer una operación de intercambio (swap) a partir de tres operadores NOT controlados (CNOT) y se asume que los CNOT son una operación primitiva en un ordenador cuántico. Un CNOT se define como

donde a y b son bits y ⊕ denota la adición módulo dos. En otras palabras, se le da la vuelta al segundo qubit si el primer qubit está en el estado |1⟩ (excitado). El subíndice “12” indica que el qubit 1 es el control y el qubit 2, el objetivo. Si intercambiamos los índices, entonces

A partir de aquí, un poco de álgebra revela que la composición de tres CNOTs implementan una operación de intercambio:

Por lo que podemos asumir que esta operación de intercambio (SWAP) está disponible entre qubits conexos.

En la figura de arriba, los qubits Q0 y Q3 no estaban directamente conectados, pero ambos estaban conectados al qubit Q2. Si intercambiamos los estados de Q0 y Q2, entonces habría ahora una conexión directa entre Q0 y Q3, y podríamos aplicar una puerta de dos qubits. Si quisiéramos, después de la puerta de dos qubits podríamos aplicar de nuevo un SWAP a Q0 y Q2 para restaurar la configuración anterior. Es fácil generalizar esto a cualquier par de qubits que tengan un camino conexo entre ellos. Esta secuencia de SWAPs se conoce como una red de SWAPs y la tarea general de “llevar los qubits a donde tienen que ir” se conoce como qubit routing (o “enrutamiento de qubits” del inglés route, “encaminar” o “dirigir”). La palabra “enrutamiento” se usa en referencia a la conmutación de paquetes en redes, por ejemplo, internet, una tarea con muchas características comunes.

Por tanto, asumiremos que podemos aplicar una puerta de dos qubits entre cualquier par de qubits. La desventaja es la cantidad de operaciones SWAP adicionales necesarias. Los ordenadores cuánticos tienen ruido y cada operación conlleva una probabilidad de error, así que cuantas más operaciones haya, más probable es que se den errores. Es por tanto de gran interés e importancia práctica desarrollar procesos que lleven a cabo el qubit routing con la menor cantidad de recursos posible, es decir, con la menor profundidad posible.

Idea principal y resultados del paper

Este paper se centra en hacer qubit routing con la menor cantidad de recursos posible y, en particular, considera un procedimiento ingenioso basado en la teleportación. Estos autores no fueron los primeros en considerar la teleportación para el qubit routing, pero lo analizan de formas novedosas. Como discutiremos más adelante, la teleportación requiere de operaciones locales (incluyendo mediciones) y de comunicaciones clásicas, abreviadas como LOCC (Local Operations and Classical Communications). Como tal, al diseño de los autores se le puede llamar enrutameinto LOCC (LOCC routing) y enrutamiento de teleportación (teleportation routing) en particular. Aquí usaremos TELE routing para referirnos al enrutamiento basado en la teleportación y SWAP routing para referirnos al basado en SWAPs.

La estrategia principal de los autores es definir métricas para cómo de bien funcionan los algoritmos de qubit routing y luego comparar el TELE routing con el SWAP routing en tres categorías principales. ¿Cuáles son las tres categorías? Un problema de enrutamiento está definido por un ordenador cuántico en el que se quiera operar y un circuito que se quiera ejecutar. De forma más abstracta, representamos un ordenador cuántico por un grafo G donde los nodos (vértices) son qubits y las aristas son conexiones entre los qubits, y representamos un circuito como una permutación π del grafo (no nos interesan las operaciones aquí, sólo cómo enrutar los qubits, por lo que basta con representar el circuito como una permutación). Por tanto, un problema de enrutamiento está definido por un grafo G y una permutación π. Las tres categorías que los autores considerar son:

Un grafo G específico y una permutación π específica.
Un grafo G específico y cualquier permutación π.
Cualquier grafo G y cualquier permutación π.

Los resultados principales en cada categoría, expresados coloquialmente, son:

Existe un grafo G con N nodos y una permutación π tales que el SWAP routing tiene una profundidad de orden N y el TELE routing tiene una profundidad constante independiente de N.
Existe un grafo G con N nodos tal que, para cualquier permutación π de G, el SWAP routing tiene una profunidad log N y el TELE routing tiene una profundidad constante independiente de N.
Para cualquier grafo G con N nodos y cualquier permutación π de G, la máxima ventaja del TELE routing sobre el SWAP routing es de orden (N log N)^½.

El resto de este artículo es una invitación a entender estos resultados, empezando por una revisión de la teleportación, pasando por los resultados más simples y dando una intuición para los otros.

Teleportación

Dado que vamos a usar la teleportación como una subrutina para el qubit routing, (re)analicemos brevemente el protocolo. El circuito cuántico para la teleportación es el que se muestra a continuación.

El circuito “teleporta” un estado cuántico arbitrario |𝜓⟩ = α|0⟩ + β|1⟩ en el primer qubit mediante operaciones locales (tanto unitarias como mediciones) y comunicación clásica. Concretamente, “comunicación clásica” significa aplicar operaciones condicionales al resultado de la medida (información clásica) en los dos primeros qubits. Dado que mandar esta información clásica no es instantáneo, el nombre “teleportación” no se puede tomar en un sentido literal.

Se puede entender el circuito de teleportación anterior como sigue. Las puertas Hadamard y CNOT crean un estado de Bell en los dos últimos qubits (omitiremos la normalización aquí y a partir de ahora).

Después, medimos los dos primeros qubits en una base de Bell, que corresponden al estado de Bell del circuito de preparación a la inversa. Antes de medir, se puede demostrar con un poco de álgebra que el estado final de los tres qubits quedaría así (de nuevo, omitiendo normalización):

Escrito de esta manera, es fácil ver cómo se podría obtener siempre el estado |𝜓⟩ en el tercer qubit después de medir los dos primeros qubits:

Si medimos |00⟩ (el primer término en la ecuación de arriba), el estado del tercer qubit es |𝜓⟩.
Si medimos |01⟩ (el segundo término), el estado del tercer qubit es X|𝜓⟩. Aplicamos X para obtener |𝜓⟩.
Si medimos |10⟩ (el tercer término), el estado del tercer qubit es Z|𝜓⟩. Aplicamos Z para obtener |𝜓⟩.
Si medimos |11⟩ (el cuarto término), el estado del tercer qubit es XZ|𝜓⟩. Aplicamos XZ para obtener |𝜓⟩.

Por tanto, siempre obtenemos |𝜓⟩ en el tercer qubit. Ahora que tenemos un dispositivo de teleportación de tres qubits, podemos considerar encadenar varios de estos dispositivos para teleportar un qubit a una mayor distancia. Esto se ilustra en la Figura 1 del paper:

Nótese la buena propiedad de que la profundidad de este circuito de siete qubits es la misma que la profundidad del circuito de teleportación de tres qubits. Específicamente, ambos circuitos tienen una profundidad de cuatro. Esto es diferente al usar el SWAP routing, en el que los SWAPs tienen que ser contiguos, como se muestra a continuación.

Aquí, la profundiad del circuito crece con el número de qubits. Esta observación es crucial para entender por qué y cuándo el enrutamiento basado en teleportación puede ser ventajoso.

Tiempo de enrutación y cotas

Sea rt(G, π) el tiempo de enrutación (profundidad mínima de circuito) necesario para aplicar la permutación π al grafo G. Sea rt(G) el tiempo de enrutación del peor caso de entre todas las permutaciones de G.

Nótese que cualquier proceso de SWAP routing puede ser “replicado” por un proceso de TELE routing que simplemente sustituye cada operación SWAP por un dispositivo de teleportación, usando la misma profundidad (constante). Sin embargo, es posible que el TELE routing sea más rápido. Por tanto, el tiempo para el TELE routing es, como mucho, el tiempo para el SWAP routing.

En un trabajo previo, se demostró que el SWAp routing en un grafo G con N nodos emplea tiempo O(N). Combinando esto con el argumento previo, también concluimos que al TELE routing le lleva tiempo O(N).

En resumen, por lo de ahora tenemos que tiempo de TELE routing ≤ tiempo de SWAP routing = O(N) en un grafo G con N nodos.

También es posible demostrar una cota inferior. Dado que intercambiar dos nodos a una distancia d requiere al menos d SWAPs, tenemos que el tiempo del SWAp routing es al menos diam(G) (el diámetro de un grafo G es la distancia máxima del camino más corto entre cualquier par de nodos). A esto se le denomina “cota inferior del diámetro” en el paper.

La cota del diámetro no aplica al TELE routing, pero es posible darle otra cota inferior. Dejando la demostración para un artículo no publicado de los mismos autores, proponen la cota

donde c(G) es la expansión de nodos de G y, para grafos conexos, vale entre 2/N y 1. LOCC routing es el más general, lo que implica que SWAP routing ≥ TELE routing ≥ 2/c(G) – 1

***TELE routing* vs *SWAP routing***

Definamos la ventaja de teleportación adv(G, π) como el cociente entre el SWAP routing y el TELE routing, es decir,

Categoría 1: un grafo G específico y una permutación específica π

El primer caso que los autores consideran es el mostrado a continuación.

Aquí tenemos un grafo lineal G (nodos negros vacíos con líneas negras como aristas) y una permutación π que intercambia el qubit más a la izquierda con el de más a la derecha. Si hay N nodos en G, el SWAP routing tiene una profundidad de orden N porque cada SWAP tiene que estar en paralelo. Sin embargo, como vimos arriba, la profundidad del TELE routing es constante en N. Por tanto, la teleportación tiene una ventaja adv(G, π) de orden N, ¡una ventaja significativa!

El segundo caso que consideran los autores es similar, mostrado a continuación.

Aquí, tenemos el mismo grafo G pero con una permutación π “en arcoíris”, llamada así porque las líneas rojas forman un arcoíris como se ve en el diagrama. El parámetro 0 < α < 1 cuantifica cuántos nodos aparecen en la permutación en arcoíris. Por la cota del diámetro, el SWAP routing tiene una profundidad N. Para el TELE routing, se pueden intercambiar cada par de nodos secuencialmente con una profundidad de circuito constante. Dado que hay N^α / 2 pares de nodos en la permutación, el TELE routing tiene una profundidad N^α / 2. Por tanto, la ventaja de la teleportación en este caso es O(N^{1 – α}). Este orden es sublinear para un α distinto de cero, así que es menos que la ventaja linear del primer caso, pero ventajoso de todos modos.

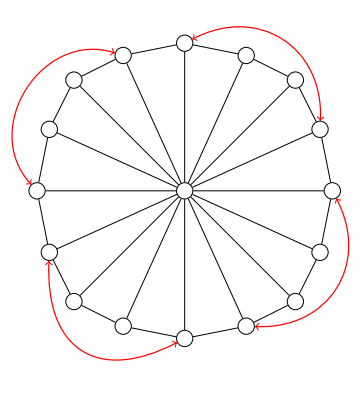
Uno puede suponer que el TELE routing solo es ventajoso porque el diámetro de los grafos lineales de los anteriores ejemplos es de orden N (el número de nodos). Pero consideremos ahora cerrar el grafo lineal de manera que los dos nudos de los extremos se conecten en un círculo. A mayores, coloquemos un nodo adicional en el centro del círculo con una arista hacia cada nodo de la circunferencia, como se muestra abajo.

El diámetro de este grafo, llamado “grafo rueda” o W_N, es constante, independientemente del número de nodos N (específicamente, el diámetro es dos). Ahora consideremos la permutación que se muestra en rojo en el grafo. Esta permutación intercambia qubits a una distancia l alrededor del “borde” de la rueda. Como los autores comentan, el tiempo del SWAP routing en este caso es min(3l, N / l – 1). El 3l se corresponde a usar el nodo central para hacer un SWAP entre cada par de qubits secuencialmente, y el N / l – 1 se corresponde a intercambiar qubits a lo largo del borde de la rueda en paralelo. Ahora bien, para el TELE routing, esta permutación sobre G se puede hacer a profundidad constante simplemente teleportando cada par de qubits a lo largo del borde en paralelo. Si tomamos l la raíz cuadrada de N / 2, esto brinda una ventaja máxima para la teleportación de

Así, el enrutamiento por teleportación permite una optimización super-diamétrica.

Categoría 2: un grafo G específico y cualquier permutación π

En el ejemplo anterior, teníamos que escoger a mano la permutación π. Ahora consideremos el caso más general de todas las permutaciones π y preguntémonos si podemos encontrar un grafo G donde el TELE routing suponga una ventaja.

Los autores muestran que la respuesta a esta pregunta resulta ser afirmativa: existe un grafo G con N nodos donde el SWAP routing tiene una profundidad al menos logarítmica en N, y el TELE routing tiene una profundidad constante independiente de N. El grafo G que lo cumple es el siguiente.

Este grafo tiene n capas de subgrafos verticalmente apiladas unas encima de otras. Como tal, los autores lo llaman L(n). La capa n-ésima es un grafo completo de 2ⁿ nodos, resaltado con aristas azules arriba. Estas capas se apilan conectando cada nodo de la capa actual con el de la capa de debajo, señalado con aristas negras arriba. Por ejemplo, la primera capa K1 tiene un nodo y una arista para cada nodo en la capa K2 de debajo. La capa K2 tiene dos nodos, y cada nodo está conectado a cada nodo de la capa K4 anterior. El número total de nodos en L(n) es 2ⁿ – 1. ¡Imagina construir un ordenador cuántico con esta topología!

Las demostraciones de las profundidades del SWAP routing y del TELE routing mencionadas anteriormente son algo complejas, por lo que las omitiremos y remitiremos al lector interesado al paper (ver Sec. V).

Categoría 3: cualquier grafo G y cualquier permutación π

Por último, los autores consideran la categoría más general de cualquier grafo G y cualquier permutación π. Para este caso, la métrica relevante es la de “máxima ventaja de teleportación”.

Los autores demuestran (Teorema 6.4) que

Luego, para cualquier ordenador cuántico con N qubits, sin importar la topología o la computación cuántica específica que queramos ejecutar, la máxima ventaja que podremos obtener usando enrutación basada en teleportación sobre la basada en SWAP será del orden de (N log N)^½. Un lector observador podría preguntarse si esto no discrepa con el primer ejemplo en la Categoría 1 donde un grafo específico G y una permutación específica π admitían una ventaja de teleportación de orden N. Sin embargo, no hay contradicción: el resultado presente considera el cociente entre las peores permutaciones, pero el resultado de la Categoría 1 considera una permutación específica.

A pesar de que es interesante desde un punto de vista teórico considerar cualquier grafo G, hay patrones comunes sobre los que se construyen los ordenadores cuántico basados en ingeniería y otras consideraciones. Por ejemplo, los qubits superconductores habitualmente se colocan en un plano bidimensional con conectividad a primeros vecinos. Los autores particularizan el resultado anterior para este caso de grafos planos y muestran que hay, como mucho, un factor constante de ventaja al usar TELE routing. Recalcamos que este resultado considera el ratio entre las peores permutaciones y no está en desacuerdo con el resultado previo sobre las permutaciones específicas. En efecto, se puede construir o dar con un circuito cuántico que se desea ejecutar en un ordenador cuántico plano para el cual el enrutamiento basado en teleportación es significativamente más práctico, aún con una mejoría de un factor constante.

Resumen y conclusiones

El problema del enrutamiento de qubits está bien justificado por consideraciones prácticas y es interesante de estudiar. Un enfoque de enrutamiento por SWAPs siempre es posible y se asemeja a ciertos problemas clásicos. Sin embargo, al igual que hay estrategias cuánticas únicas e ingeniosas para subrutinas como la adición en un ordenador cuántico, hay una estrategia única e ingeniosa para el enrutamiento de qubits basada en la teleportación. Es fácil construir ejemplos donde el enrutamiento basado en teleportación es ventajoso y los autores proporcionan afirmaciones generales sobre su rendimiento en relación al SWAP routing. A pesar de que en términos generales, la ventaja es como mucho (N log N)^½ para un ordenador cuántico de N qubits – y como mucho constante para grafos planos – muy probablemente existen casos prácticos en los que el enrutamiento basado en teleportación es seguramente ventajoso. Así que, la próxima vez que estés considerando los aspectos prácticos de cómo se podría ejecutar un algoritmo en un ordenador cuántico, ¡recuerda la teleportación como estrategia para el enrutamiento de qubits!