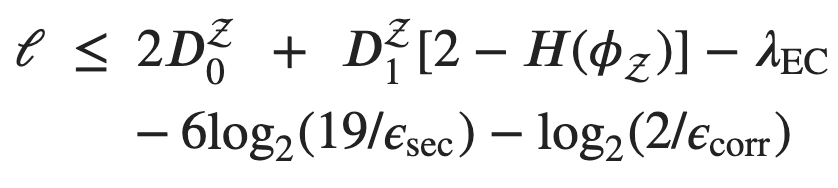QuBytes

Fluxonium Qubits Show Promise in Modern Quantum Computer Architectures

Title: High-fidelity two-qubit gates on fluxoniums using a tunable coupler

Authors: Ilya N. Moskalenko, Ilya A. Simakov, Nikolay N. Abramov, Alexander A. Grigorev, Dmitry O. Moskalev, Anastasiya A. Pishchimova, Nikita S. Smirnov, Evgeniy V. Zikiy, Ilya A. Rodionov & Ilya S. Besedin

Institutions:

National University of Science and Technology ‘MISIS’, Moscow, Russia; Russian Quantum Center, 143025, Skolkovo, Moscow, Russia
Moscow Institute of Physics and Technology, 141701, Dolgoprudny, Russia
Dukhov Research Institute of Automatics (VNIIA), Moscow, 127055, Russia
FMN Laboratory, Bauman Moscow State Technical University, Moscow, 105005, Russia

Manuscript: Published 08 November 2022 on Nature

Note: This is part of a series of articles written as final projects for Physics 438b at USC.

Background and Motivation

Currently, in the realm of quantum computers and quantum devices, there is an ongoing search for better system architectures to improve reliability and mitigate information loss when performing operations on qubits. These efforts are essential for the advancement of quantum computing, as qubits are inherently fragile and susceptible to decoherence and other unwanted effects. Decoherence occurs when a qubit interacts with its environment in such a way that the original state becomes mixed or entangled with the states of its surroundings. If decoherence occurs, we lose valuable information about a system and cannot perform high-precision operations.

Many recent quantum processor designs involve the implementation of two-qubit gate systems, where transmon qubits serve as the fundamental element upon which quantum gates operate. In quantum circuits, these gates serve as the building blocks that perform operations on the qubits. Transmon qubits, created by a small superconducting island (an island being a region of some superconducting material) connected to a reservoir by a Josephson junction, have been extensively researched in the past decade and are a popular choice for quantum computing. They exhibit low levels of decoherence in comparison to other qubit architectures, enabling transmons to maintain a certain quantum state for a longer period, thus allowing for more reliable operation results. Even so, transmon qubits still have some information loss; for example, they can have lower gate fidelities, which are a measure of how accurately the qubit performs as a quantum gate. Although some transmon qubit systems have almost perfect fidelity (two-qubit systems have been shown to have gate fidelities of ~99.5% according to various demonstrations), there are still other concerns. Crosstalk, the phenomenon in which a quantum state of one qubit affects another, leads to computational errors and decreases the reliability of transmon qubits. Transmon qubits are particularly susceptible to a specific type of crosstalk known as static ZZ interaction, which is a specific type of persistent and undesired coupling that can lead to decoherence and qubit frequency/state shifts.

Because of these challenges, alternative two-qubit architectures with fewer situations for decoherence to occur along with higher gate fidelities are being explored. One type of qubit, known as a fluxonium, is gaining traction in quantum processors and is the subject of this article. Specifically, a fluxonium two-qubit gate system where the qubits are paired to a tunable capacitive coupler could be a novel way of developing scalable NISQ (Noisy Intermediate-Scale Quantum) devices.

Fluxonium Qubits

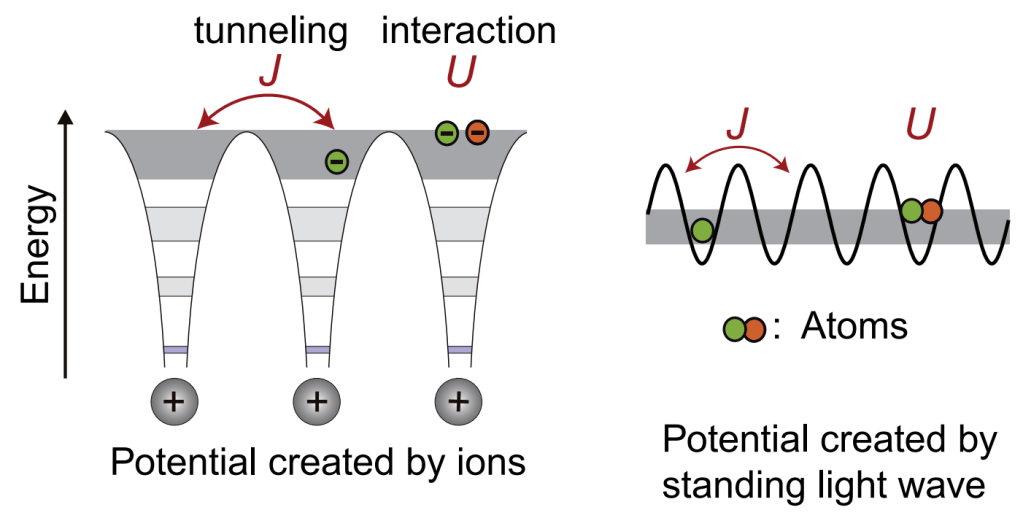
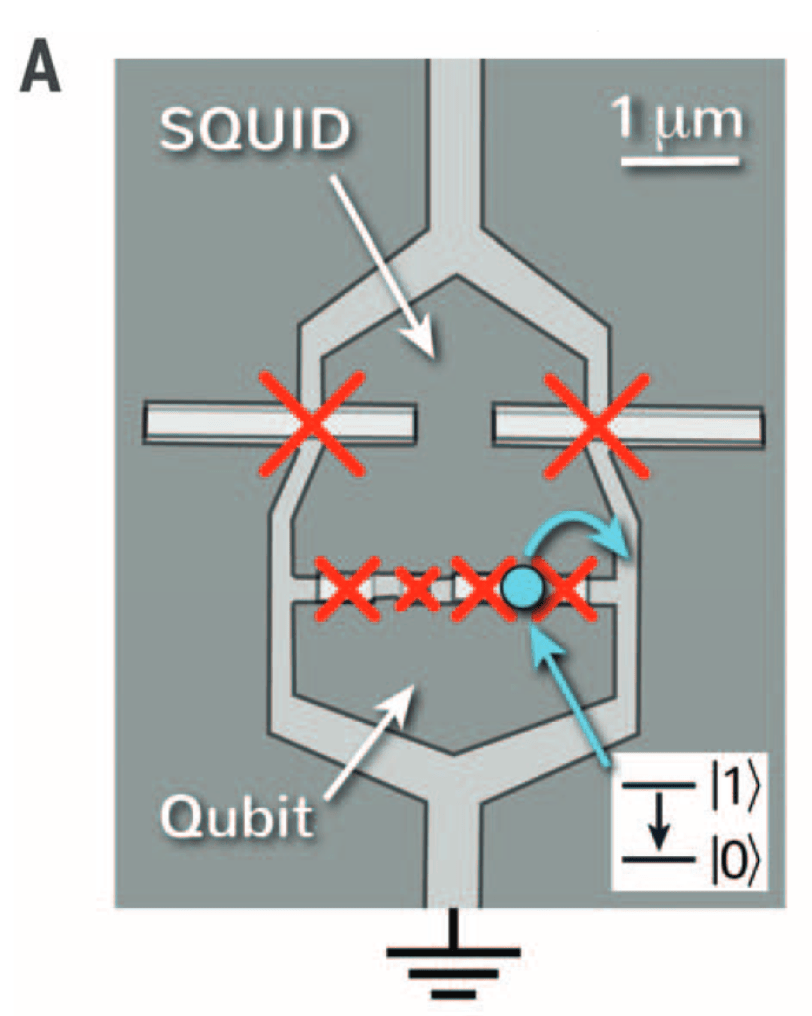
Fluxonium qubits consist of a superconducting loop—different from transmon’s superconducting island—interrupted by a Josephson junction. The Josephson junction has a weak insulating barrier that allows pairs of electrons (called Cooper pairs) to tunnel through it, and through this tunneling, the qubit’s quantum state can be manipulated. When a current is applied to the superconducting loop, it creates a magnetic flux that becomes trapped by the junction. This magnetic flux is quantized, meaning it is discrete in value and can exist only in certain allowed states. These discrete states form the basis of the quantum states of the qubit, and they can be manipulated using quantum gates to perform operations in a quantum computer.

Just like transmon qubits, fluxonium qubits have high gate fidelities and long coherence times, allowing them to maintain a state for a long time without decaying to another state. Fluxonium qubits also have a better level of control over states versus the transmon qubits. Importantly, these qubits are characterized by a lower frequency than transmon qubits. These (resonant) frequencies dictate how the qubit can be manipulated when specific control signals are applied. Fluxonium qubits are also more resistant to information loss and noise, although static ZZ interactions are still a critical issue.

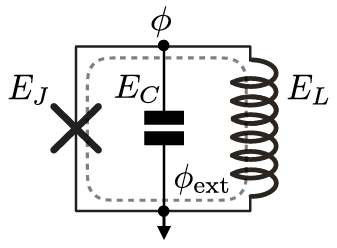
Figure 1: Schematic of a fluxonium qubit, featuring the Josephson junction ( $E_{J}$ ), the central conductor ( $E_{C}$ ), and the inductor ( $E_{L}$ ). The addition of the inductor is basically a step up from the transmon qubit.⁴

Figure 1: Schematic of a fluxonium qubit, featuring the Josephson junction ( $E_{J}$ ), the central conductor ( $E_{C}$ ), and the inductor ( $E_{L}$ ). The addition of the inductor is basically a step up from the transmon qubit.⁴

Adding a tunable coupler…

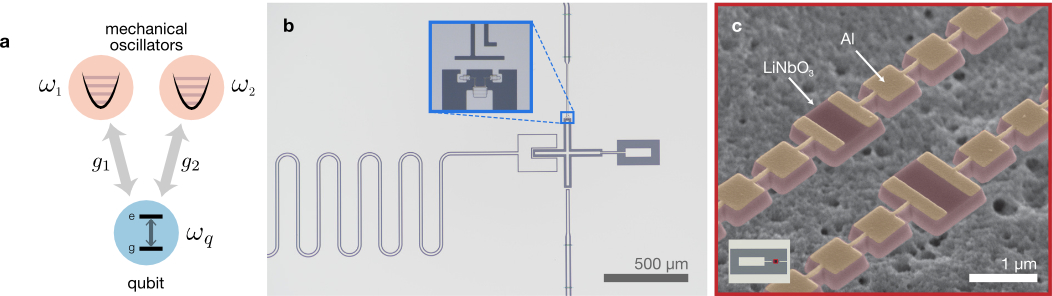
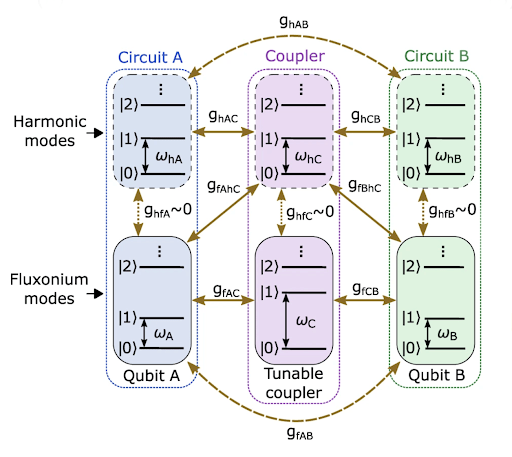
In order to simultaneously increase the gate fidelity and suppress static ZZ interaction in the two-qubit gate processor, the researchers created a processor (see Figure 3) featuring two modified fluxonium circuits (with extra harmonic modes so, therefore, more resonant frequencies) with a central tunable capacitive coupler in which the coupler’s frequencies are controlled by individual fast flux bias lines that are directly electrically connected (galvanically). These are just a type of superconducting circuit that controls the magnetic flux in a qubit. The flux control/bias lines are prone to issues if not developed and implemented carefully; the most relevant issues being attenuation and filtering. Attenuation refers to the loss of signal strength as a control signal transfers through a flux control line which affects the accuracy of the control (since it is difficult to get the sought-after control signal to the qubit). Filtering refers to the removal of unwanted frequencies and noise: if not well designed, it can also remove frequencies from the control signal, which affects reliability. In the case of this article, the individual galvanization allows for independent control of magnetic flux in each bias line. This method of implementing tunable coupling in a quantum computer using capacitive coupling relies on the phenomenon of charge transfer between two objects due to their proximity, to control the interactions between qubits. In this architecture, the qubits are arranged in a specific configuration that allows for this capacitive coupling. By making small adjustments to the distance between the qubits (as well as the size and shape of what they are made of), it is possible to control the strength of the capacitive coupling between them. Just as the qubits have their own frequencies (Qubit A: $\omega_{A}/2\pi$ = 688.224 MHz, and qubit B: $\omega_{B}/2\pi$ = 664.763 MHz), so does the coupler; in fact, the harmonic frequency of the coupler is $\omega_{hc}/2\pi$ = 2.0 GHz, and this can also be controlled via galvanically coupled fast flux bias lines.²

Figure 2: Schematic of the two-qubit gate and coupler system. Circuits A and B are used as data qubits, while the coupler remains in the ground state to reduce the possibility of extra decoherence.²

Figure 3: Schematic of the circuit. The readout is where observation occurs, and the “X”s represent Josephson junctions.²

Now, with some careful manipulation to reduce the degrees of freedom of the system, the effective-low energy Hamiltonian of this two-qubit processor becomes:

${\hat{H}}_{{{{\rm{eff}}}}}/\hbar =-\frac{1}{2}{\omega }_{{{{\rm{A}}}}}{\sigma }_{{{{\rm{A}}}}}^{{{{\rm{z}}}}}-\frac{1}{2}{\omega }_{{{{\rm{B}}}}}{\sigma }_{{{{\rm{B}}}}}^{{{{\rm{z}}}}}+{g}_{{{{\rm{xx}}}}}{\sigma }_{{{{\rm{A}}}}}^{{{{\rm{x}}}}}{\sigma }_{{{{\rm{B}}}}}^{{{{\rm{x}}}}}+\frac{1}{4}{\zeta }_{{{{\rm{zz}}}}}{\sigma }_{{{{\rm{A}}}}}^{{{{\rm{z}}}}}{\sigma }_{{{{\rm{B}}}}}^{{{{\rm{z}}}}}$

Notice that this Hamiltonian includes two ‘qubit terms’ and some additional ones as well; the third term relates to the coupling, and the fourth term relates to the ZZ interaction!

Time for Quantum Gates

From here, universal gates, which are a set of logical operations that can be used to create any other logical operation, were implemented on the processor using specific pulse sequences. Specifically, the CZ gate and a variation of the iSWAP gate (called the √iSWAP-like gate) were chosen for this purpose; both of these choices derive from what is known as the fSim family. The fSim family is a group of quantum algorithms based on the original fSim (fermionic simulation) algorithm which simulates several different quantum systems, including gates. fSim can be represented with a matrix in the $\left| 00 \right\rangle, \left| 01 \right\rangle, \left| 10 \right\rangle, \left| 11 \right\rangle$ basis which describes a series of rotations that operate on different states:

$\text{fSim}(\theta, \phi) = \begin{pmatrix}1 & 0 & 0 & 0 \\ 0 & \cos \theta & -i\sin \theta & 0 \\ 0 & -i\sin \theta & \cos \theta & 0 \\ 0 & 0 & 0 & e^{-i\phi}\end{pmatrix}$

Where the swap angle $\theta$ determines the strength of the coupling between two qubits, and is a phase shift parameter that is only applied when the two-qubit state is $\left| 11 \right\rangle$ . This conditional phase shift technique is used to fine-tune qubits’ behavior during specific operations and manipulations.

With this in mind, the qubit-qubit coupling term ${g}_{{{{\rm{xx}}}}}$ was measured by applying $\pi$ pulses—controlled electromagnetic pulses of a specific duration and amplitude used to rotate qubit states by 180 degrees—to one of the qubits followed by a modulated flux pulse in order to bring that qubit and the other qubit into resonance. Pulses of magnetic flux are used to control the states of these qubits; these pulses are applied using the galvanized flux control lines mentioned previously, which apply a magnetic field to the qubit in a controlled and accurate way. Calibrating gates this way using sets of flux pulses allowed for the quantification of ${g}_{{{{\rm{xx}}}}}$ against ${{{\Phi }}}_{{{{\rm{C}}}}}^{{{{\rm{x}}}}}$ , which represents various square-shaped flux pulses sent through the coupler bias line.

Figure 4: Graph of ${{{\Phi }}}_{{{{\rm{C}}}}}^{{{{\rm{x}}}}}$ vs ${g}_{{{{\rm{xx}}}}}$ /2pi. Notice that there is a region of steadiness from -0.4 to 0.4 flux offset ${{{\Phi }}}_{{{{\rm{C}}}}}^{{{{\rm{x}}}}}$ .²

Figure 4: Graph of ${{{\Phi }}}_{{{{\rm{C}}}}}^{{{{\rm{x}}}}}$ vs ${g}_{{{{\rm{xx}}}}}$ /2pi. Notice that there is a region of steadiness from -0.4 to 0.4 flux offset ${{{\Phi }}}_{{{{\rm{C}}}}}^{{{{\rm{x}}}}}$ .²

The researcher’s √iSWAP-like gate (with $\theta = -\pi/4$ , or fSim( $-\pi/4, \phi$ ) used was implemented using rabi oscillations, which are essentially time-dependent electromagnetic field drives, and were enacted between the $\left|10\right\rangle$ and $\left|01\right\rangle$ states. This √iSWAP-like gate was specifically done by tuning to a specific amount, waiting for a portion of a Rabi cycle, and then detuning back to the original frequency.¹ These oscillations modify ${g}_{{{{\rm{xx}}}}}$ in the processor Hamiltonian above.

The CZ (controlled-Z) gate, which was also included in testing because of various precision-related drawbacks the √iSWAP-like gate alone has, was created with two fSim ( $\theta = -\pi/4$ ) gates and five single-qubit gates. The CZ gate takes two qubits as input and applies a Z gate to the second single qubit if the first qubit is in the state $\left|1\right\rangle$ . This rotates the state of that qubit around the z-axis of the Bloch sphere. This is reminiscent of entangled states given that the second qubit will only be rotated if the first qubit is in a specific state.

Next, using the coupler flux bias lines, researchers introduced flux pulses that enabled them to precisely modulate the flux. This flux modulation allowed for the qubits to come into resonance. As mentioned previously, these fluxonium qubits operated at a lower frequency than transmon qubits, which allowed the researchers to perform more operations within a period of time without the qubit decaying to a lower state.

Experimental Results

After the implementation of both of these processes, through experiment, it was discovered the static ZZ interaction was almost entirely eliminated (less than 1 kHz remaining!) over a wide range of magnetic fluxes because of the addition of the tunable coupler and the ability to precisely control ${g}_{{{{\rm{xx}}}}}$ . This is an extremely valuable result given the ZZ interaction causes decoherence and decreases the reliability of operations on quantum processors.

As for gate fidelities of the CZ and √iSWAP-like gates, each was verified using a method called cross-entropy benchmarking (XEB).³ XEB is an algorithm that involves preparing a particular quantum state, performing a specific set of manipulations via various measurement operators, and then analyzing the output of said manipulations probabilistically in comparison to the same state and operations on another (reference) processor/system. In relation to XEB, a parameter called “circuit depth,” which is easiest related to the complexity of a circuit: the greater the depth, the more difficult and resource-consuming the system may be to implement on a quantum computer. Typically it is best practice to minimize this value, although experimentally it was varied to show how the fidelity exponentially decreased as circuit depth increased.

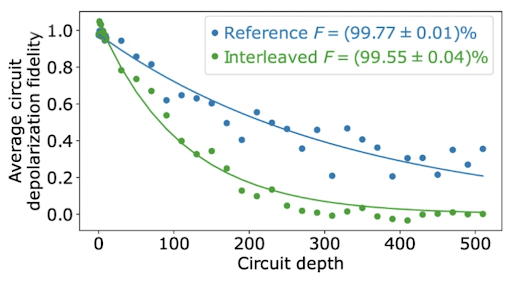
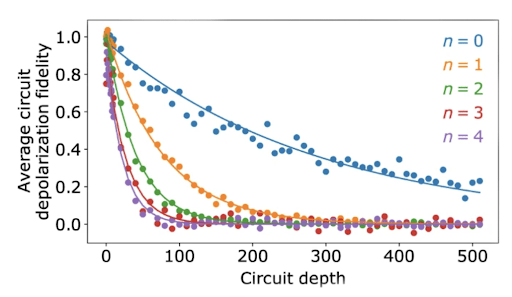
Figure 5: Reference F represents the depolarization fidelity of the reference system, which in this case, was random single-qubit gate sequences on two qubits. The Interleaved F represents the depolarization fidelity of our intended system including the fSim gate (in the case of the √iSWAP-like gate).²

For the √iSWAP-like gate, its resulting gate fidelity was measured to be F = (99.55 ± 0.04)%, as Figure 5 represents with interleaved F. Meanwhile, the CZ gate fidelities were tested using different numbers of CZ gates in a linear sequence; experimentally, the greater the number (n) of CZ gates in sequence, the lower the average circuit depolarization fidelity (see Figure 6). For a single CZ gate alone, the fidelity was measured to be F = (99.22 ± 0.03)%.

Figure 6: CZ gate fidelities, where $n$ corresponds to the number of CZ gates in a linear sequence.²

Conclusion

In confirming significant static ZZ suppression as well as gate fidelities greater than previously recorded in comparison to processors composed of transmon qubits, it is evident that this processor architecture composed of fluxonium qubits with a tunable capacitive coupler shows that fluxonium qubits are a promising alternative to the popular transmon option in regards to the creation of a quantum processor in which qubits remain in a single state for a longer period of time while maintaining resistance to crosstalk. These two characteristics are essential for the development of future scalable quantum computers. Hopefully, given this success, fluxonium qubits will receive greater attention and experimentation in the near future.

References

¹Moskalenko, I. N., Besedin, I. S., Simakov, I. A. & Ustinov, A. V. Tunable coupling scheme for implementing two-qubit gates on fluxonium qubits. Appl. Phys. Lett. 119, 194001 (2021).

² Moskalenko, I.N., Simakov, I.A., Abramov, N.N. et al. High fidelity two-qubit gates on fluxoniums using a tunable coupler. npj Quantum Inf 8, 130 (2022).

³Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).

⁴Nguyen, L. B. et al. The high-coherence fluxonium qubit. American Physical Society 9, 4 (2019).

Observing Particle Exchange Phases with Two-Photon Interference: the Hong-Ou-Mandel Effect

Title: Hong-Ou-Mandel Interference between Two Hyper-Entangled Photons Enables Observation of Symmetric and Anti-Symmetric Particle Exchange Phases

Authors: Zhi-Feng Liu, Chao Chen, Jia-Min Xu, Zi-Mo Cheng, et al.

Manuscript: Published 23 December 2022 on Physical Review Letters, [1]

Note: this is part of a series of articles written as final projects for Physics 438b at USC

What is the Hong-Ou-Mandel Effect?

Two-photon interference, termed the Hong-Ou-Mandel (HOM) effect, has been hailed for being fundamentally quantum with no classical counterpart since its first observation roughly 30 years ago. It is usually implemented with an optical device essential to optical quantum information processing systems, a Beam Splitter (BS), a cube-like instrument as shown below in Fig.1.(a). A beam incident on the BS will be split between two output ports with certain transmittance and reflectance parameters; here we consider the 50:50 BS, where transmittance and reflectance are balanced, thus the incident particle is equally possible to arrive at either of the output ports (for 50:50 BS and different output possibilities, see the right panel of Fig.1).

The HOM effect occurs when two indistinguishable photons (those with the same parameters such as wavelength and polarization) are incident at the two input ports, one at each, as the two photons will always come out at the same port. Such interference manifests itself as a dip centered at 0.0 delay on the output graph plotting numbers of coincidences to the delay in emitting the two particles: when they arrive at the same time, they interfere with each other and thus change the output possibilities. A dip is the “bunching” effect as zero coincidence events could be observed when the input particles are bosons that can occupy the same quantum state at the same time according to the Pauli exclusion principle; if they are fermions that cannot, there is observed a peak or an “anti-bunching” result (see Fig.2 and (a) and (b) of Fig.3).

The key to the “quantumness” of the HOM effect comes in at both particle-wave duality and indistinguishability of the photons, which are bosons; two identical photons always arrive at the same output port, since their indistinguishability requires them to be identical in all potential measurements.

Figure 1: Taken from Bouchard et al. (2020) [2]. (a) Labeled a and b are the input ports, while c and d are the output ports; (b) four different possible trajectories of two photons.

Quantum entanglement therefore is inherently linked to the HOM effect, both critical to quantum information processing procedures. Entanglement of two particles can be conveniently prepared with the Bell states: four maximally entangled states that constitute an orthonormal basis to the two-dimensional Hilbert space. If not identical, two photons can differ in a number of different degrees of freedom (DoFs): horizontal or vertical polarization, timing, frequency, or spatial modes. Take polarization as an example, the Bell states are:

$\vert \phi^{\pm} \rangle_{12} = \frac{1}{\sqrt{2}}(\vert H \rangle_{1} \vert H \rangle_{2} \pm \vert V \rangle_{1} \vert V \rangle_{2})$
$\vert \psi^{\pm} \rangle_{12} = \frac{1}{\sqrt{2}}(\vert H \rangle_{1}\vert H \rangle_{2} \pm \vert V \rangle_{1}\vert V \rangle_{2})$

Where H and V represent the horizontal and vertical polarization states, and subscripts denote particles 1 and 2. Out of the four, only one has exchange anti-symmetry where swapping the subscripts 1 and 2 lead to an extra minus sign on the overall state:

$\vert \psi^{-} \rangle_{21}= -\vert \psi^{-}\rangle_{12}$

This state is the Fermion state, where though photons are bosons, their difference in polarization allows states with fermionic qualities as above. The Fermion state exhibits the anti-bunching effect, and the other three states are Boson states that exhibit the bunching effect; picture (a) of Fig.2 illustrates this relationship.

Motivation and the New Idea

One of the key challenges to testing HOM interference experimentally in settings more generalized than identical photons is how to prepare the symmetry or anti-symmetry that the effect relies on. As illustrated above, using the Bell states as input is a convenient solution. Prior to Liu et al. (2022), all the current state-of-the-art experimental research has been limited to using the Bell-state entanglement in only one DoF. But applying the HOM interference in higher dimensions or more DoFs has been an active area of new research: though we will not go into details about them, recently there have been interesting reports on engineering generalized HOM interference with spatial modes (see Hiekkamäki and Fickler (2021) [6]) and structured light along with semi-conductor chips (see Francesconi et al. (2020) [5]).

Liu et al. (2022) presented a way to experimentally explore the HOM interference in two DoFs, adding a DoF of orbital angular momentum (OAM) to the polarization degree, as shown in the right column of (a) in Fig.2. Bell-states hyper-entangled (maximally entangled) photons are utilized in their experiment in order to manipulate the symmetry of the two-photon states.

Moreover, by extending the Hilbert space with one more DoF in OAM, Liu et al. were able to devise a way to control the OAM DoF exchange with the entangled polarization states. In this way they successfully related the external exchange phase in OAM, an initially unmeasurable quantity, into measurable internal phases, thus able to measure the external exchange phase. The concept and implementation scheme of their measurements is explained in the following section.

Setting Up Two-Photon Interference with Two Degrees of Freedom

First, express the initial states of our two photons with a degree of freedom in the OAM, similar to what we did with polarization in the first section. Orbital angular momentum of a particle along a given axis is the magnetic quantum number $m$ ; here we take the value of $m$ as a label and let each photon have OAM of $\pm m\hbar$ . Their Bell states are thus written as:

$\vert \mu^{\pm}\rangle_{12} = \frac{1}{\sqrt{2}}(\vert +m \rangle_{1}\vert +m \rangle_{2} \pm \vert -m \rangle_{1}\vert -m \rangle_{2})$
$\vert \nu^{\pm}\rangle_{12} = \frac{1}{\sqrt{2}}(\vert +m \rangle_{1}\vert -m \rangle_{2} \pm \vert -m \rangle_{1}\vert +m \rangle_{2})$

Where $+m$ and $-m$ correspond to $\pm m\hbar$ , and $\vert \nu^{-}_{12} \rangle$ is the Fermion state (also shown as the 4th state in (a) of Fig.2).

Figure 2: Taken from Liu et al. (2022) [1]. (a) Diagram showing the procedure of two-photon interference in one DoF, respectively with a polarization DoF and an OAM DoF, starting from the Bell states. The first three states are Boson states, and the last is the Fermion state; (b) Diagram showing the procedure of HOM interference in two DoFs, starting with sixteen different ways of hyper-entanglement between Bell states.

Now to conduct the generalized HOM effect experiment in two DoFs, we write the states of the two hyper-entangled photons as tensor products of the respective Bell states for each DoF, a way to express the combination of two independent states denoted by ⊗. Since there are four Bell states for each DoF in the two entangled photons, in combination we have sixteen different hyper-entangled states. Depending on whether the states are bosonic or fermionic in each DoF, those 16 states can be divided into four groups. The number, names, and tensor products of these states are shown below:

(1) Fermion-Fermion state: $\vert \psi^{-}\rangle \otimes \vert \nu^{-}\rangle$
(3) Fermion-Boson state: $\vert \psi^{-}\rangle \otimes \{\vert \mu^{+}\rangle, \vert \mu^{-}\rangle, \vert \nu^{+}\rangle \}$
(3) Boson-Fermion state: $\{\vert \phi^{+}\rangle, \vert \phi^{-}\rangle, \vert \psi^{+}\rangle \} \otimes \vert \nu^{-}\rangle$
(9) Boson-Fermion state: $\{\vert \phi^{+}\rangle, \vert \phi^{-}\rangle, \vert \psi^{+}\rangle \} \otimes \{\vert \mu^{+}\rangle, \vert \mu^{-}\rangle, \vert \nu^{+}\rangle\}$

If a state is a product of two Fermion or two Boson states, we classify it as an even state; if a state is a product of one Fermion state and one Boson state, we classify it as an odd state. This categorization of even or odd, sometimes called “parity of states,” determines the exchange symmetry or antisymmetry, and thus determines the observed HOM effects. Theoretically, it predicts that even states should give the bunching effect like two identical bosons, and odd states should give the anti-bunching effect.

Fig.3 illustrates the results Liu et al. obtained from their two-photon interference experiment in two DoFs, in curves of photon counts to delay. They define a quantity, a way of measuring how pronounced the peak or dip is, called the “extracted visibility of an interference” as:

$V_{dip} = 1 - \frac{C_0}{C_\infty}$
$V_{peak} = \frac{C_0}{C_\infty} - 1$

Where C₀is the fitted count of photons at 0.0 delay, and C_∞is the fitted count at infinite delay. From their observed data, the extracted visibility of the peaks and dips ranges from 0.902 ± 0.071 to 0.993 ± 0.002, all relatively pronounced. As could also be seen straight from the graph, six peaks resulted from the three Fermion-Boson and three Boson-Fermion states, and ten dips resulted from the one Fermion-Fermion and nine Boson-Boson states, just as the exchange symmetry theory would have predicted!

Figure 3: Taken from Liu et al. (2022) [1]. (a) and (b) are 2-photon counts plotted against delay for respectively polarization and OAM Bell states; (c) is 2-photon counts plotted against delay for HOM interference in two DoFs. Error bars are smaller than data spheres.

Measuring the Exchange Phase

Liu et al. also proposed that their enactment of the two-DoF two-photon interference can be applied to directly measure the particle exchange phase of the two photons, by introducing a supplementary DoF and creating a superposition between states. To better understand how their measurement works, we’ll first consider the exchange process of a normal two-photon OAM entangled state. The exchange can be written as a unitary evolution process, a process that doesn’t change the magnitude of the state:

$\vert OAM \rangle_{12} \xrightarrow{exchange} \vert OAM \rangle_{21} = e^{j\Phi_O} \vert OAM \rangle_{12}$

Where we say Φ_Ois the “exchange phase,” and $\vert OAM \rangle_{12}$ refers to all of the possible OAM states. Note that the OAM state here doesn’t have to be a Bell state, but only one of the Bell states will give an exchange phase of π. For a Boson state in OAM, exchanging the two photons does not make a difference on the overall state, thus Φ_Oshould be 0; on the contrary, for a Fermion state the exchanged state acquires a minus sign, so Φ_Oshould equal to π (exchange anti-symmetric phase) only in the $\vert \nu^{-} \rangle$ state of two photons.

In order to create superposition between states in the two different DoFs and extract the external exchange phase, now the authors add on another degree of freedom in polarization, and set up a process to utilize this reference DoF in directly measuring the exchange phase. The designed process is illustrated in Fig.4. They first prepare initial hyper-entangled states with one Boson state in the polarization DoF and an OAM state:

$\frac{1}{\sqrt{2}}(\vert H \rangle_{1}\vert H \rangle_{2} + \vert V \rangle_{1}\vert V \rangle_{2}) \otimes \vert OAM \rangle_{12}$

Then pass this state through an optical device named a polarization beam splitter (PBS), which passes the first term in the above state with horizontal polarizations through the splitter intact, but reflects the second term or the vertical polarization components into an exchange. After that, for the vertical polarization components, the OAM portion picks up its usual exchange phase written out above, and the polarization portion picks up an exchange phase Φ_Pthat is known and could be experimentally dealt with by being passed through a Babinet Compensator (BC). As its name indicates, the BC compensates for the polarization exchange phase, returning to its initial both-horizontal-polarization state, but keeping the OAM part intact. I’ll represent this whole process in the equation below:

$\vert V \rangle_{1}\vert V \rangle_{2} \otimes \vert OAM \rangle_{12}$
$\xrightarrow{PBS} e^{j\pi}\vert V \rangle_{2}\vert V \rangle_{1} \otimes \vert OAM \rangle_{21} = e^{j(\pi +\Phi_P)}\vert V \rangle_{1}\vert V \rangle_{2} \otimes e^{j\Phi_O} \vert OAM \rangle_{12}$
$\xrightarrow{BC} \vert V \rangle_{1}\vert V \rangle_{2} \otimes e^{j\Phi_O} \vert OAM \rangle_{12}$

Overall, the initial state will become:

$\frac{1}{\sqrt{2}}(\vert H \rangle_{1}\vert H \rangle_{2} + \vert V \rangle_{1}\vert V \rangle_{2}) \otimes \vert OAM \rangle_{12}$
$\xrightarrow{PBS+BC} \frac{1}{\sqrt{2}}(\vert H \rangle_{1}\vert H \rangle_{2} + e^{j\Phi_O} \vert V \rangle_{1}\vert V \rangle_{2}) \otimes \vert OAM \rangle_{12}$

It is evident that the problem of measuring the external, or global, exchange phase of the OAM is now turned into the much easier problem of measuring the internal phase, or ratio between $\vert H \rangle_{1} \vert H \rangle_{2}$ and $\vert V \rangle_{1} \vert V \rangle_{2}$ . With the aid of entanglement in the prepared polarization Bell state, we don’t need to measure anything related to the OAM state itself anymore.

Figure 4: Taken from Liu et al. (2022) [1]. Diagram showing the scheme of using two hyper-entangled photons, linking one polarization state with any OAM state, sending the beam through a PBS and a BC discussed above, and thus resulting in a superposition state that transform the measurement of the global exchange phase into the internal phase in the polarization DoF.

To acquire the ratio between horizontal and vertical polarization states, Li et al. projected the polarization state of the two photons onto two sets of states. Both sets are combinations of the state photon 1 is projected onto and one of the states photon 2 is projected onto. The specific combinations are shown below:

Photon 1 projected on: $\frac{1}{\sqrt{2}} (\vert H \rangle_{1} + \vert V \rangle_{1})$
Photon 2 projected on: $\frac{1}{\sqrt{2}} (\vert H \rangle_{1} \pm e^{j\theta} \vert V \rangle_{1})$

Where the basis for photon 1 primarily functions to leave all of the effects from the OAM particle exchange to photon 2. Photon 2, on the other hand, is projected onto the eigenstates of an observable M_θdefined as follows:

$M_\theta = cos\theta \sigma_x + sin\theta \sigma_y$

Where σ_xand σ_yare respectively the x and y Pauli matrices. The angle θ is a quantity that could be determined in the lab by the orientation of one of the devices used, and could thus be varied by altering that orientation. To get to M_θthen from Li et al’s experiment, start from the photon counts on the two bases and calculate them into relative probabilities P_±. The expectation value of M_θcan now be calculated as the difference between the probabilities: P₊− P₋.

According to theory, when the value of θ equals the global exchange phase angle we aim to measure, the observable M_θwould reach 1, its maximum value. To confirm the theory, Li et al fed the four different Bell states of OAM into their setup, and the computed values of M_θfrom these four experiments are plotted against the θ angles in Fig.5. As predicted, the three exchange phases or θ values are very close to 0 for the three Boson states, and the exchange phase for the Fermion state is $1\pi$ . Since their behavior confirms theoretical predictions, now we are able to directly measure the exchange phases by varying θ to achieve M_θ= 1.

Figure 5: Taken from Liu et al. (2022) [1]. The expectation value of *M_θ*, difference of the relative probabilities of two-photon counts in two bases of measurement, is plotted against the angle θ varied and measured in the lab, and error bars are smaller than data points.

Summary and Implication

There have been attempts to generalize the Hong-Ou-Mandel effect to higher degrees of freedom for a few decades now, motivated by its inherent connection with entanglement, the heart of cutting-edge research on quantum information. In this paper, researchers have for the first time systematically, successfully generalized the HOM two-photon interference to two degrees of freedom with two hyper-entangled photons. Their work informs potential new directions and developments for quantum information sciences: the usage of hyper-entanglement provides a method of direct measurement of the exchange phases using an extra DoF that could be generalized to different or more DoFs. Again, we won’t go into the details of them, but the authors have suggested their work could be useful in exploring ideas like alignment-free quantum communications (where the sender and receiver of information no longer need to be aligned) (see D’ambrosio et al. (2012) [3]) and complete Bell state measurements (see Ecker et al. (2021) [4]). In addition, with the aid of new techniques in preparing maximum entanglement in higher dimensions, the HOM effect might be also tested using similar methods in higher dimension and applied to information processing in general.

References

[1] Liu, Z.-F., Chen, C., Xu, J.-M., Cheng, Z.-M., Ren, Z.-C., Dong, B.-W., . . . others. (2022). Hong-ou-mandel interference between two hyperentangled photons enables observation of symmetric and antisymmetric particle exchange phases. Physical Review Letters, 129 (26), 263602.

[2] Bouchard, F., Sit, A., Zhang, Y., Fickler, R., Miatto, F. M., Yao, Y., . . . Karimi, E. (2020). Two-photon interference: the hong–ou–mandel effect. Reports on Progress in Physics, 84 (1), 012402.

[3] D’ambrosio, V., Nagali, E., Walborn, S. P., Aolita, L., Slussarenko, S., Marrucci, L., & Sciarrino, F.(2012). Complete experimental toolbox for alignment-free quantum communication. Nature communications, 3 (1), 1–8.

[4] Ecker, S., Sohr, P., Bulla, L., Huber, M., Bohmann, M., & Ursin, R. (2021). Experimental single-copy entanglement distillation. Physical Review Letters, 127 (4), 040506.

[5] Francesconi, S., Baboux, F., Raymond, A., Fabre, N., Boucher, G., Lemaitre, A., . . . Ducci, S. (2020). Engineering two-photon wavefunction and exchange statistics in a semiconductor chip. Optica, 7 (4), 316–322.

[6] Hiekkamäki, M., & Fickler, R. (2021). High-dimensional two-photon interference effects in spatial modes. Physical Review Letters, 126 (12), 123601.

Enrutamiento cuántico con teleportación

Por Ryan LaRose

Este post ha sido patrocinado por Tabor Electronics. Para mantenerte al día con los productos y aplicaciones de Tabor, únete a su comunidad en LinkedIn y suscríbete a su newsletter.

Autores: Dhruv Devulapalli, Eddie Schoute, Aniruddha Bapat, Andrew M. Childs, Alexey V. Gorshkov

arXiv: https://arxiv.org/abs/2204.04185

Contexto y motivación

Cuando escribimos circuitos cuánticos en papel o en software, es conveniente asumir que cualquier par de qubits están conectados. Es conveniente tanto para (i) alcanzar un nivel de abstracción – a veces no queremos pensar sobre detalles de hardware a bajo nivel cuando pensamos en algoritmos – como para (ii) porque es en cierta manera verdad – incluso si no hay una arista directa entre dos qubits, mientras haya algún camino conexo, los qubits pueden interactuar. Esto se muestra en la figura a continuación.

En el panel de la izquierda, la figura muestra un procesador superconductor de cinco qubits de IBMQ y en el panel de la derecha, se destacan las conexiones entre los qubits. Los qubits Q0 y Q1 están directamente conectados, pero los qubits Q0 y Q3 no lo están. Sin embargo, hay un camino conexo entre el qubit Q0 y el Q3, es decir, el camino Q0 – Q2 – Q3. Dado que este camino conexo existe, se pueden aplicar operaciones de dos qubits entre los qubits Q0 y Q3.

¿Cómo es esto posible? Intercambiar dos qubits es una operación unitaria – en efecto, es una operación autoinversa – y por tanto, una operación cuántica permitida. Además, se puede presuponer que es una operación disponible en un ordenador cuántico. De hecho, podemos componer una operación de intercambio (swap) a partir de tres operadores NOT controlados (CNOT) y se asume que los CNOT son una operación primitiva en un ordenador cuántico. Un CNOT se define como

donde a y b son bits y ⊕ denota la adición módulo dos. En otras palabras, se le da la vuelta al segundo qubit si el primer qubit está en el estado |1⟩ (excitado). El subíndice “12” indica que el qubit 1 es el control y el qubit 2, el objetivo. Si intercambiamos los índices, entonces

A partir de aquí, un poco de álgebra revela que la composición de tres CNOTs implementan una operación de intercambio:

Por lo que podemos asumir que esta operación de intercambio (SWAP) está disponible entre qubits conexos.

En la figura de arriba, los qubits Q0 y Q3 no estaban directamente conectados, pero ambos estaban conectados al qubit Q2. Si intercambiamos los estados de Q0 y Q2, entonces habría ahora una conexión directa entre Q0 y Q3, y podríamos aplicar una puerta de dos qubits. Si quisiéramos, después de la puerta de dos qubits podríamos aplicar de nuevo un SWAP a Q0 y Q2 para restaurar la configuración anterior. Es fácil generalizar esto a cualquier par de qubits que tengan un camino conexo entre ellos. Esta secuencia de SWAPs se conoce como una red de SWAPs y la tarea general de “llevar los qubits a donde tienen que ir” se conoce como qubit routing (o “enrutamiento de qubits” del inglés route, “encaminar” o “dirigir”). La palabra “enrutamiento” se usa en referencia a la conmutación de paquetes en redes, por ejemplo, internet, una tarea con muchas características comunes.

Por tanto, asumiremos que podemos aplicar una puerta de dos qubits entre cualquier par de qubits. La desventaja es la cantidad de operaciones SWAP adicionales necesarias. Los ordenadores cuánticos tienen ruido y cada operación conlleva una probabilidad de error, así que cuantas más operaciones haya, más probable es que se den errores. Es por tanto de gran interés e importancia práctica desarrollar procesos que lleven a cabo el qubit routing con la menor cantidad de recursos posible, es decir, con la menor profundidad posible.

Idea principal y resultados del paper

Este paper se centra en hacer qubit routing con la menor cantidad de recursos posible y, en particular, considera un procedimiento ingenioso basado en la teleportación. Estos autores no fueron los primeros en considerar la teleportación para el qubit routing, pero lo analizan de formas novedosas. Como discutiremos más adelante, la teleportación requiere de operaciones locales (incluyendo mediciones) y de comunicaciones clásicas, abreviadas como LOCC (Local Operations and Classical Communications). Como tal, al diseño de los autores se le puede llamar enrutameinto LOCC (LOCC routing) y enrutamiento de teleportación (teleportation routing) en particular. Aquí usaremos TELE routing para referirnos al enrutamiento basado en la teleportación y SWAP routing para referirnos al basado en SWAPs.

La estrategia principal de los autores es definir métricas para cómo de bien funcionan los algoritmos de qubit routing y luego comparar el TELE routing con el SWAP routing en tres categorías principales. ¿Cuáles son las tres categorías? Un problema de enrutamiento está definido por un ordenador cuántico en el que se quiera operar y un circuito que se quiera ejecutar. De forma más abstracta, representamos un ordenador cuántico por un grafo G donde los nodos (vértices) son qubits y las aristas son conexiones entre los qubits, y representamos un circuito como una permutación π del grafo (no nos interesan las operaciones aquí, sólo cómo enrutar los qubits, por lo que basta con representar el circuito como una permutación). Por tanto, un problema de enrutamiento está definido por un grafo G y una permutación π. Las tres categorías que los autores considerar son:

Un grafo G específico y una permutación π específica.
Un grafo G específico y cualquier permutación π.
Cualquier grafo G y cualquier permutación π.

Los resultados principales en cada categoría, expresados coloquialmente, son:

Existe un grafo G con N nodos y una permutación π tales que el SWAP routing tiene una profundidad de orden N y el TELE routing tiene una profundidad constante independiente de N.
Existe un grafo G con N nodos tal que, para cualquier permutación π de G, el SWAP routing tiene una profunidad log N y el TELE routing tiene una profundidad constante independiente de N.
Para cualquier grafo G con N nodos y cualquier permutación π de G, la máxima ventaja del TELE routing sobre el SWAP routing es de orden (N log N)^½.

El resto de este artículo es una invitación a entender estos resultados, empezando por una revisión de la teleportación, pasando por los resultados más simples y dando una intuición para los otros.

Teleportación

Dado que vamos a usar la teleportación como una subrutina para el qubit routing, (re)analicemos brevemente el protocolo. El circuito cuántico para la teleportación es el que se muestra a continuación.

El circuito “teleporta” un estado cuántico arbitrario |𝜓⟩ = α|0⟩ + β|1⟩ en el primer qubit mediante operaciones locales (tanto unitarias como mediciones) y comunicación clásica. Concretamente, “comunicación clásica” significa aplicar operaciones condicionales al resultado de la medida (información clásica) en los dos primeros qubits. Dado que mandar esta información clásica no es instantáneo, el nombre “teleportación” no se puede tomar en un sentido literal.

Se puede entender el circuito de teleportación anterior como sigue. Las puertas Hadamard y CNOT crean un estado de Bell en los dos últimos qubits (omitiremos la normalización aquí y a partir de ahora).

Después, medimos los dos primeros qubits en una base de Bell, que corresponden al estado de Bell del circuito de preparación a la inversa. Antes de medir, se puede demostrar con un poco de álgebra que el estado final de los tres qubits quedaría así (de nuevo, omitiendo normalización):

Escrito de esta manera, es fácil ver cómo se podría obtener siempre el estado |𝜓⟩ en el tercer qubit después de medir los dos primeros qubits:

Si medimos |00⟩ (el primer término en la ecuación de arriba), el estado del tercer qubit es |𝜓⟩.
Si medimos |01⟩ (el segundo término), el estado del tercer qubit es X|𝜓⟩. Aplicamos X para obtener |𝜓⟩.
Si medimos |10⟩ (el tercer término), el estado del tercer qubit es Z|𝜓⟩. Aplicamos Z para obtener |𝜓⟩.
Si medimos |11⟩ (el cuarto término), el estado del tercer qubit es XZ|𝜓⟩. Aplicamos XZ para obtener |𝜓⟩.

Por tanto, siempre obtenemos |𝜓⟩ en el tercer qubit. Ahora que tenemos un dispositivo de teleportación de tres qubits, podemos considerar encadenar varios de estos dispositivos para teleportar un qubit a una mayor distancia. Esto se ilustra en la Figura 1 del paper:

Nótese la buena propiedad de que la profundidad de este circuito de siete qubits es la misma que la profundidad del circuito de teleportación de tres qubits. Específicamente, ambos circuitos tienen una profundidad de cuatro. Esto es diferente al usar el SWAP routing, en el que los SWAPs tienen que ser contiguos, como se muestra a continuación.

Aquí, la profundiad del circuito crece con el número de qubits. Esta observación es crucial para entender por qué y cuándo el enrutamiento basado en teleportación puede ser ventajoso.

Tiempo de enrutación y cotas

Sea rt(G, π) el tiempo de enrutación (profundidad mínima de circuito) necesario para aplicar la permutación π al grafo G. Sea rt(G) el tiempo de enrutación del peor caso de entre todas las permutaciones de G.

Nótese que cualquier proceso de SWAP routing puede ser “replicado” por un proceso de TELE routing que simplemente sustituye cada operación SWAP por un dispositivo de teleportación, usando la misma profundidad (constante). Sin embargo, es posible que el TELE routing sea más rápido. Por tanto, el tiempo para el TELE routing es, como mucho, el tiempo para el SWAP routing.

En un trabajo previo, se demostró que el SWAp routing en un grafo G con N nodos emplea tiempo O(N). Combinando esto con el argumento previo, también concluimos que al TELE routing le lleva tiempo O(N).

En resumen, por lo de ahora tenemos que tiempo de TELE routing ≤ tiempo de SWAP routing = O(N) en un grafo G con N nodos.

También es posible demostrar una cota inferior. Dado que intercambiar dos nodos a una distancia d requiere al menos d SWAPs, tenemos que el tiempo del SWAp routing es al menos diam(G) (el diámetro de un grafo G es la distancia máxima del camino más corto entre cualquier par de nodos). A esto se le denomina “cota inferior del diámetro” en el paper.

La cota del diámetro no aplica al TELE routing, pero es posible darle otra cota inferior. Dejando la demostración para un artículo no publicado de los mismos autores, proponen la cota

donde c(G) es la expansión de nodos de G y, para grafos conexos, vale entre 2/N y 1. LOCC routing es el más general, lo que implica que SWAP routing ≥ TELE routing ≥ 2/c(G) – 1

***TELE routing* vs *SWAP routing***

Definamos la ventaja de teleportación adv(G, π) como el cociente entre el SWAP routing y el TELE routing, es decir,

Categoría 1: un grafo G específico y una permutación específica π

El primer caso que los autores consideran es el mostrado a continuación.

Aquí tenemos un grafo lineal G (nodos negros vacíos con líneas negras como aristas) y una permutación π que intercambia el qubit más a la izquierda con el de más a la derecha. Si hay N nodos en G, el SWAP routing tiene una profundidad de orden N porque cada SWAP tiene que estar en paralelo. Sin embargo, como vimos arriba, la profundidad del TELE routing es constante en N. Por tanto, la teleportación tiene una ventaja adv(G, π) de orden N, ¡una ventaja significativa!

El segundo caso que consideran los autores es similar, mostrado a continuación.

Aquí, tenemos el mismo grafo G pero con una permutación π “en arcoíris”, llamada así porque las líneas rojas forman un arcoíris como se ve en el diagrama. El parámetro 0 < α < 1 cuantifica cuántos nodos aparecen en la permutación en arcoíris. Por la cota del diámetro, el SWAP routing tiene una profundidad N. Para el TELE routing, se pueden intercambiar cada par de nodos secuencialmente con una profundidad de circuito constante. Dado que hay N^α / 2 pares de nodos en la permutación, el TELE routing tiene una profundidad N^α / 2. Por tanto, la ventaja de la teleportación en este caso es O(N^{1 – α}). Este orden es sublinear para un α distinto de cero, así que es menos que la ventaja linear del primer caso, pero ventajoso de todos modos.

Uno puede suponer que el TELE routing solo es ventajoso porque el diámetro de los grafos lineales de los anteriores ejemplos es de orden N (el número de nodos). Pero consideremos ahora cerrar el grafo lineal de manera que los dos nudos de los extremos se conecten en un círculo. A mayores, coloquemos un nodo adicional en el centro del círculo con una arista hacia cada nodo de la circunferencia, como se muestra abajo.

El diámetro de este grafo, llamado “grafo rueda” o W_N, es constante, independientemente del número de nodos N (específicamente, el diámetro es dos). Ahora consideremos la permutación que se muestra en rojo en el grafo. Esta permutación intercambia qubits a una distancia l alrededor del “borde” de la rueda. Como los autores comentan, el tiempo del SWAP routing en este caso es min(3l, N / l – 1). El 3l se corresponde a usar el nodo central para hacer un SWAP entre cada par de qubits secuencialmente, y el N / l – 1 se corresponde a intercambiar qubits a lo largo del borde de la rueda en paralelo. Ahora bien, para el TELE routing, esta permutación sobre G se puede hacer a profundidad constante simplemente teleportando cada par de qubits a lo largo del borde en paralelo. Si tomamos l la raíz cuadrada de N / 2, esto brinda una ventaja máxima para la teleportación de

Así, el enrutamiento por teleportación permite una optimización super-diamétrica.

Categoría 2: un grafo G específico y cualquier permutación π

En el ejemplo anterior, teníamos que escoger a mano la permutación π. Ahora consideremos el caso más general de todas las permutaciones π y preguntémonos si podemos encontrar un grafo G donde el TELE routing suponga una ventaja.

Los autores muestran que la respuesta a esta pregunta resulta ser afirmativa: existe un grafo G con N nodos donde el SWAP routing tiene una profundidad al menos logarítmica en N, y el TELE routing tiene una profundidad constante independiente de N. El grafo G que lo cumple es el siguiente.

Este grafo tiene n capas de subgrafos verticalmente apiladas unas encima de otras. Como tal, los autores lo llaman L(n). La capa n-ésima es un grafo completo de 2ⁿ nodos, resaltado con aristas azules arriba. Estas capas se apilan conectando cada nodo de la capa actual con el de la capa de debajo, señalado con aristas negras arriba. Por ejemplo, la primera capa K1 tiene un nodo y una arista para cada nodo en la capa K2 de debajo. La capa K2 tiene dos nodos, y cada nodo está conectado a cada nodo de la capa K4 anterior. El número total de nodos en L(n) es 2ⁿ – 1. ¡Imagina construir un ordenador cuántico con esta topología!

Las demostraciones de las profundidades del SWAP routing y del TELE routing mencionadas anteriormente son algo complejas, por lo que las omitiremos y remitiremos al lector interesado al paper (ver Sec. V).

Categoría 3: cualquier grafo G y cualquier permutación π

Por último, los autores consideran la categoría más general de cualquier grafo G y cualquier permutación π. Para este caso, la métrica relevante es la de “máxima ventaja de teleportación”.

Los autores demuestran (Teorema 6.4) que

Luego, para cualquier ordenador cuántico con N qubits, sin importar la topología o la computación cuántica específica que queramos ejecutar, la máxima ventaja que podremos obtener usando enrutación basada en teleportación sobre la basada en SWAP será del orden de (N log N)^½. Un lector observador podría preguntarse si esto no discrepa con el primer ejemplo en la Categoría 1 donde un grafo específico G y una permutación específica π admitían una ventaja de teleportación de orden N. Sin embargo, no hay contradicción: el resultado presente considera el cociente entre las peores permutaciones, pero el resultado de la Categoría 1 considera una permutación específica.

A pesar de que es interesante desde un punto de vista teórico considerar cualquier grafo G, hay patrones comunes sobre los que se construyen los ordenadores cuántico basados en ingeniería y otras consideraciones. Por ejemplo, los qubits superconductores habitualmente se colocan en un plano bidimensional con conectividad a primeros vecinos. Los autores particularizan el resultado anterior para este caso de grafos planos y muestran que hay, como mucho, un factor constante de ventaja al usar TELE routing. Recalcamos que este resultado considera el ratio entre las peores permutaciones y no está en desacuerdo con el resultado previo sobre las permutaciones específicas. En efecto, se puede construir o dar con un circuito cuántico que se desea ejecutar en un ordenador cuántico plano para el cual el enrutamiento basado en teleportación es significativamente más práctico, aún con una mejoría de un factor constante.

Resumen y conclusiones

El problema del enrutamiento de qubits está bien justificado por consideraciones prácticas y es interesante de estudiar. Un enfoque de enrutamiento por SWAPs siempre es posible y se asemeja a ciertos problemas clásicos. Sin embargo, al igual que hay estrategias cuánticas únicas e ingeniosas para subrutinas como la adición en un ordenador cuántico, hay una estrategia única e ingeniosa para el enrutamiento de qubits basada en la teleportación. Es fácil construir ejemplos donde el enrutamiento basado en teleportación es ventajoso y los autores proporcionan afirmaciones generales sobre su rendimiento en relación al SWAP routing. A pesar de que en términos generales, la ventaja es como mucho (N log N)^½ para un ordenador cuántico de N qubits – y como mucho constante para grafos planos – muy probablemente existen casos prácticos en los que el enrutamiento basado en teleportación es seguramente ventajoso. Así que, la próxima vez que estés considerando los aspectos prácticos de cómo se podría ejecutar un algoritmo en un ordenador cuántico, ¡recuerda la teleportación como estrategia para el enrutamiento de qubits!

Big Step For Quantum Communication

Title: Path-encoded high-dimensional quantum communication over a 2-km multicore fiber

Authors: Beatrice Da Lio, Daniele Cozzolino, Nicola Biagi, Yunhong Ding, Karsten Rottwitt, Alessandro Zavatta, Davide Bacco, and Leif K. Oxenløwe

Manuscript: Published April 22 2012 in Nature

Note: this part of a series of articles written as final projects for Physics 438b at USC

Introduction

There is and will always be a constant need for ‘better’ ways to communicate information across states, borders, and seas. The recent work done by Beatrice Da Lio and her team regarding the most effective modes of transmission of quantum key distribution (QKD) protocol has given us a look into what the future may hold for communication and the transmission of information. Specifically, their paper, “Path-encoded high-dimensional quantum communication over a 2-km multicore fiber,” covers how their work looks at the transmission to a core of a multicore fiber is thus far the best candidate for carrying out high-speed QKD protocol.

What even is QKD anyway? Broadly speaking, it is a very secure way to exchange encryption keys from one place to the next via principles of quantum mechanics. This is far different than what we know and use daily, as QKD relies solely on quantum mechanics instead of mathematical calculations. This is done through the use of qubits, otherwise referred to by their longer name; quantum bits, which are the quantum counterpart to the commonly used bit which computers use to store information. To carry this out, a sender, in this work, we refer to the sender as Alice, encodes an encryption key in the form of many different quantum states, typically as polarized photons to a receiver, Bob. It is then left to Bob to take those quantum states, measure them, and then take those measurements and remake the original key that was sent from Alice. However, the work done in this paper takes this general sender and receiver setup and explains the most effective and efficient way to transmit and carry this out.

How they did it

When going forth to manufacture a far more efficient and fast transmission of information, there are issues that need to be addressed. In this paper, the authors explored the use of higher-dimensional qubits, called qudits, to improve the transmission’s functionality by reducing both noise and errors. They considered two options for transmission: coupling each path to a single-mode fiber or each to a multicore fiber. The first option was susceptible to phase drifts caused by temperature and mechanical stress, thus leading to more errors. The second option, using a multicore fiber (MCF), delivered better results with fewer errors but was only workable at very short distances. The authors found that using qudits in the dimension d=4, or ququarts, allowed for efficient transmission with little error at a distance of 2 km. This is a promising start for future transmission efforts, but how did they do it?

In order to avoid the issue of phase drifts, there needed to be a decent amount of work. These phase drifts lead to the disruption of the phase coherence of the superposition of these states, so it is crucial to eliminate the chance of any drifts taking place. This is exactly why the authors decided that the use of MCF’s as the primary mode of transmission; they allowed for a slower rate of phase drifts, but at the cost of requiring a form of stabilization signal as well. Specifically, the authors’ work uses a phase-locked loop (PLL) to actually stabilize drifts in the channels. Sadly, no such thing is bound to be completely perfect and PLL’s do have the chance of not being able to correct the errors quickly enough due to the photons sent traveling at the speed of light. If multiple phase drifts were to occur, without the proper stabilization, the two signals may get mixed up without ever being able to be fixed. Two different types of stabilization are required to prevent errors: one consisting of an independent stabilization and transmission channel, and the second which uses a stabilization loop that uses the errors on the states as a reference signal through the use of an actuator.

Now to allow for the random state choice, the stabilization channel is integrated with a fast optical phase modulation of the states which requires two mutually unbiased bases shown in Figure 1 below:

Figure 1. From “Path-encoded high-dimensional quantum communication over a 2-km multicore fiber”, Da Lio, Beatrice, et al. 2021 These are the two bases used for their work.

There are 8 total states which live on a superposition of just two of the cores, as well as having a pi phase difference to make work easier with the help of a phase modulator (PM). There are going to be a handful of names, do bear with me. Signals need to travel the same optical path as the stabilization channel and must be transmitted in the same fiber to allow for the phase drifts to be properly stabilized. However, as the stabilization signal is phase modulated, there are

interference fringes that happen due to the phase-locked loop (PLL) that cannot be seen, this is the issue involving interference fringes that occur when a stabilization signal is phase modulated. Thus, there needed to be a way to ensure that the interference fringes can then become visualized. The solution involves exploiting the “polarization dependence of PM crystals,” by aligning the polarization of the stabilization signal to be orthogonal to the phase modulator’s modulation axis. This allows for the interference fringes to be seen, and the use of a phase modulation loop (PML), shown in Figure 2 below, is then employed to achieve the desired output.

Figure 2. From “Path-encoded high-dimensional quantum communication over a 2-km multicore fiber”, Da Lio, Beatrice, et al. 2021. This is the setup of the phase modulation loop which the work uses. The PML consists of a quantum channel (indicated by the red arrow), a stabilization channel (indicated by the blue arrow), a single-mode fiber (indicated by the yellow fiber), a polarization-maintaining fiber (indicated by the blue fiber), a polarizing beam splitter (PBS), a phase modulator (PM), and a polarization controller (PC).

The PML uses the components as depicted in Figure 2 to modulate the phase of the stabilization signal in order to make the interference fringes visible and improve the output. At the end of this process, both of the signals traveling in their respective loops, they will be directed to the PBS’s second input, and it now falls onto Alice to take on the rest.

As we already mentioned, the bulk of the transmission of the information is carried out by Alice, the sender, and Bob, the receiver. However, Alice is tasked with preparing the quantum states and transmitting them simultaneously with the stabilization signal to Bob, via the MCF. This must be done carefully to ensure that the signals are sent out at the same time and that there are no phase drifts. Bob then measures both of the transmitted states and uses them to stabilize the channel. This process is crucial for ensuring the security and dependability of the communication.

Figure 3. From “Path-encoded high-dimensional quantum communication over a 2-km multicore fiber”, Da Lio, Beatrice, et al. 2021. The entire setup for the work done, it is made up of a quantum channel (indicated by the red arrow), a stabilization channel (indicated by the blue arrow), an intensity modulator (IM), beam splitters (BS), an optical switch (SWITCH), a variable optical attenuator (VOA), a phase modulation loop (PML), a multicore fiber (MCF), a phase shifter (PS), a phase-locked loop board (PLL), wavelength division multiplexing filters (F), and various detectors, including superconducting nanowire single-photon detectors (D1, D2, D3, and D4) and InGaAs single-photon detectors (D5 and D6). This is what is used in the transmission of the quantum states between Alice and Bob to stabilize the channel to ensure both the security and reliability of the communication.

The PMLs mentioned above are positioned following the beam splitters to complete the stabilization of signals just prior to being transmitted through the 2km MCF. On the opposite side, or Bob’s side, PLLs are subsequently utilized to stabilize the signals received by Bob. This setup involves the use of two continuous-wave lasers, one for each the quantum and stabilization channel. The light from the first laser is attenuated and turned into a train of pulses, and then these are used by Alice to prepare the quantum states. The stabilization signal is also attenuated and sent through the MCF. Once they reach Bob, the quantum states are measured using superconducting nanowire single-photon detectors, where the stabilization signal is utilized to compensate for possible phase drifts. The entirety of this setup is controlled by a field-programmable gate array board, and the counts from the detectors themselves are then collected by a time tagger. After going through the alphabet soup of components, it all falls upon Bob to just measure both states and continue stabilizing the channel, honestly not too much to ask.

Quantum Protocol

Now, let’s step away from the technicalities of the experimental setup and look at what the authors were able to do with the setup and information from above. After running multiple tests over various periods of time, the team deduced that the best outcomes of transmission were those carried out over a 1-hour period. While 1 hour is nowhere near the rapid speeds that would be necessary for the future commercial and personal use of QKD, nevertheless, this outcome is immensely important for pathing the way for future work to be built upon their findings.

Shown in Figure 4 below is the QBER over time, where the QBER is the ratio between the wrong detections and total detections.

Figure 4. From“Path-encoded high-dimensional quantum communication over a 2-km multicore fiber”, Da Lio, Beatrice, et al. 2021. This is their data produced over a 1-hour time period.

In red are the results from the X basis configuration, and how the stabilization system instated is able to both track the random phase drifts and compensate for them. This depicts all the stable data, the good stuff we want. The spikes in Figure 4 show times when the PLL lost the locking position. From their data, they were able to determine that using just the switch modulation may result in clear, stable output, however, the output due to the phase modulator does get impacted by phase drifts so this one does end up requiring some form of stabilization to account for those. In the top right corner of Figure 4, there is a zoomed-in portion of the lower part of the graph; from this, we can see that the data points in red are consistently 0.02 higher than the yellow. This indicates what the contribution from the QBER is to be. The average contribution to the QBER from both the stabilization and the phase modulator is 2.8%, thus overall, the study provides good data on the impact of phase drifts on QKD systems.

The QKD protocol used here is specifically done through the use of a 4-D path-encoded BB84 scheme by using weak coherent pulses (pulses with the same frequency and phase). The authors use a decoy method to counter the photon number-splitting attack. They find that using

three different intensities for the decoy method is optimal, but using two intensities is more practical. The authors also discuss the impact of phase drifts on the output and the need for stabilization to account for these drifts. Overall, the study provides good data on QKD using weak coherent pulses. For the 4-D QKD protocol, they must use the bound 4-D secret key with one decoy, here they use the following equation to define their ideal secret key length, ℓ as shown in Figure 5.

Figure 5. From“Path-encoded high-dimensional quantum communication over a 2-km multicore fiber”, Da Lio, Beatrice, et al. 2021. Depicted is the equation used to define their ideal secret key length.

This secret key length is defined in the paper as being the “number of secret key bits created in a privacy amplification block of length n_z.” The following variables are defined: D₀Z and D₁^Zare the lower bounds for the vacuum and the single photon events that occur in the Z basis, H is the function of the high-dimensional entropy where ϕ is the upper bound of the phase error in the Z-basis, λ_ECis the number of bits that end up being discarded during the error correction process, ε_secis the secrecy parameter, and lastly, ε_corris the correctness parameter. Now they needed to derive the secret key rate that their setup could achieve, to do so, they had the following fixed values: n_Z= 10⁹bit and ε_sec= ε_corr= 10⁻¹⁵. As well as the two values for the 2 intensities which were found to be the most optimal (μ₁and μ₂). Here, Pμ₁is the probability of Alice sending a state with the intensity μ₁and P_Zis the probability that Alice will choose to prepare in the Z basis OR that Bob will measure in the Z basis. They found the following values for the parameters, which were used for all 4 possible configurations:

1. Z basis and intensity μ₁

2. Z basis and intensity μ₂

3. X basis and intensity μ₁

4. X basis and intensity μ₂

After their 1-hour period of running their setup, they obtained the following table in Figure 6. From the data points here, they were able to use their secret key length to determine the secret key rate to be: R_sk≈ 6.3 Mbit/s. This value was compared to prior work and found that before the secret key rate was ≈ 3.7 Mbit/s, thus showing their work was able to nearly double the prior rate!

Figure 6. From “Path-encoded high-dimensional quantum communication over a 2-km multicore fiber”, depicting the table of their acquired data.

To get to this value of 6.3 Mbit/s, they, again, used the system shown below and repeated multiple runs for roughly 93 seconds each. This repetition of 93 seconds is the time that was required to create the privacy amplification block, nz. However, in order to replicate their results over much longer transmission distances, they assumed that the signals would experience similar phase drifts. They then used this assumption to emulate the effects of phase drifts at longer distances and added more attenuation to the channel using a variable optical attenuator (VOA).

Now the authors took their work and compared it to the simulations to see how their work fit in. Below is Figure 7, depicting the quantum bit error rate, and this graph shows both simulated and experimental data for the Z and X bases for intensities μ1 and μ2. The uncertainty values are computed as the standard error of the mean. The simulation data is represented by solid lines, and the experimental values are represented by yellow squares and blue triangles. Here, the squares and triangles represent the Z and X bases, respectively.

Figure 7. From Path-encoded high-dimensional quantum communication over a 2-km multicore fiber, depicting the graphs of their channel losses versus QBER.

Next, Figure 8 below depicts the channel loss in decibels versus the secret key rate in bits/second. The blue lines depict the simulated values and the orange dots are their experimental values. It is rather clear that these graphs show quite the agreement between the simulated and experimental results!

Figure 8. From Path-encoded high-dimensional quantum communication over a 2-km multicore fiber, showing a graph between the simulation and experimental secret key rates and channel loss.

In Summary

The work which the authors conducted has been able to demonstrate the efficacy of the usage of multicore fibers in combination with a ququart-based system for quantum key distribution. Their work is carried out through the use of a phase-locked loop system to aid in reducing the number of errors caused by phase drifts. To go in hand with phase-locked loop systems, stabilization was required in the form of making use of the polarization dependence that most of the equipment used to encode the quantum states acquired, as well as employing a decoy method and real-time basis choice as other vital components. A comparison of their results to prior work on qubit systems finds that their ququart system has a higher secret key rate. The National Security Agency explains that future uses for high-speed QKD protocol will have major developments in areas such as cybersecurity, but the path to reach this point is a very long one. However, it is evident that further work needs to be carried out on farther transmission distances to make this system commercially viable.

References

Da Lio, Beatrice, et al. “Path-Encoded High-Dimensional Quantum Communication over a 2-Km Multicore Fiber.” Npj Quantum Information, vol. 7, no. 1, 2021, pp. 1–6, https://doi.org/10.1038/s41534-021-00398-y. 

“Quantum Key Distribution (QKD) and Quantum Cryptography (QC).” National Security Agency/Central Security Service > Cybersecurity > Quantum Key Distribution (QKD) and Quantum Cryptography QC, https://www.nsa.gov/Cybersecurity/Quantum-Key-Distribution-QKD-and-Quantum-Cryp tography-QC/.

Simulating the early Universe on a table top Quantum Simulator

By: Shaurya Bhave

Authors: Bo Song¹, Shovan Dutta¹, Shaurya Bhave¹, Jr-Chiun Yu¹, Edward Carter¹, Nigel Cooper² & Ulrich Schneider¹

Institution: 1) Cavendish Laboratory, University of Cambridge, Cambridge, UK
2) Department of Physics and Astronomy, University of Florence, Sesto Fiorentino, Italy.

Manuscript: Published in Nature Physics [4]

The natural world is host to several systems that exist in one or more phases. These phases are typically separated by a transition, often triggered by thermal fluctuations. A few prominent examples are phases of water, ferromagnetism in solids, and superconducting phases in strongly interacting systems such as high-temperature superconductors. These phases are typically separated by a transition and can typically be classified as either discontinuous or continuous.

Fig 1: Visualization of the difference between a continuous and a discontinuous phase transition. The two phases are modelled as two states in a double well potential. The transition to the alternate ground state can happen in two different ways. The first allows the state to change seamlessly from one to the other, whilst the other changes the potential abruptly, resulting in metastability. — **Fig 1:** Visualization of the difference between a continuous and a discontinuous phase transition. The two phases are modelled as two states in a double well potential. The transition to the alternate ground state can happen in two different ways. The first allows the state to change seamlessly from one to the other, whilst the other changes the potential abruptly, resulting in metastability.

Whether the transition is discontinuous or continuous depends on the path taken to change over from one state of the system to another. This is illustrated in Fig. 1, where the initial state changes seamlessly to the other in the case of a continuous one.

This is usually reflected in continuous change of the order parameter as parameters are swept through the transition point.

A discontinuous transition is characterized by a sudden change in the order parameter as the transition is crossed. The lack of a smooth change results in a phenomenon known as metastability (see Fig. 1). Metastability is the tendency of a global phase to persist despite crossing the transition point, indicating the existence of two stable equilibrium points.

Typically, these phase transitions are classical, as they are caused by thermal fluctuations. The most familiar example is the phase transitions of water. There also exist more complex transitions, such as the ferromagnetic to paramagnetic transition and the transition responsible for superconductivity.

The microscopic behaviour of the latter two systems is determined by quantum mechanics. However, the transition itself is classical. It is the result of thermal fluctuations within the system, as the temperature is reduced below a critical point.

A further distinction can be made between phase transitions that are driven by thermal fluctuations and those driven by quantum fluctuations. The latter are referred to as quantum phase transitions. Quantum phase transitions occur close to T = 0, and are mostly seen in degenerate quantum degenerate matter, such as the electron gas in metals.

Many studies usually focus on continuous phase transitions, as they are the most common form of quantum phase transitions. However, discontinuous transitions have been gaining interest for their relevance in the evolution of the early universe, where some studies suggest that the universe evolved from a hot plasma to its current state by multiple phase transitions [1, 2]. Various models have been proposed, which contend that these transitions were discontinuous; they occurred through the decay of a metastable state [3].

The study, carried out by lead author Bo Song [4], realized a quantum system which hosts a metastable state and displays a discontinuous phase transition. In this experiment, they tune this quantum phase transition from a continuous transition to a discontinuous transition and demonstrate the metastability of this state. This work builds on previous proposals for using ultracold atoms as a table top simulator of the early universe [5, 6] and opens the possibility to study the quantum decay of metastable states.

A table top Quantum Simulator

The aim of a quantum simulator is to study the behavior of a system governed by the laws of quantum mechanics such as solid-state systems. Often, the phenomenon of interest in these systems is clouded by unwanted effects, such as those of temperature and impurities in the case of metals. Due to these challenges in traditional solid-state experiments, one can instead use a simulation (to capture the same principal results).

However, simulating these on classical computers becomes difficult, because the Hilbert space needed to encode these computations increases exponentially with the size of the system.

This motivates the need for a quantum simulator. These can be of two types: digital or analog. Digital simulators decompose the evolution of the system into a series of operations called quantum gates (akin to logic gates). These gates are then implemented on a quantum computer – an assembly of qubits.

An alternative approach is to create a different physical system which is governed by quantum mechanics. This is where one creates an analogous system whose Hamiltonian maps onto the system you want to study. One example of an analog simulator ultracold atoms in optical lattices, which naturally realize the physical characteristic of electrons in periodic solids. It should be noted that digital simulator platforms- such as superconducting circuits [7] – have also been used in similar manners to implement lattice type physics.

**Fig 2:** In a quantum simulator the metal is approximated with an analog system. The potential wells of an optical lattice (sinusoidal potential on the right) map onto those of the potential wells created by the metallic ions. Whilst this is a simplification, the advantage is that one can tune the tunnelling and the interactions freely by simply modifying the laser power. Figure taken from [10].

An analog simulator is engineered to be highly controllable, and free of any unwanted effects. The high tunability gives the experimenter full control over the critical parameters of the Hamiltonian. This allows the experimenter to directly observe quantum states and ground state phases. In traditional solid-state experiments, signatures of different phases are probed indirectly, but with quantum simulators, one can directly observe phase transitions like magnetism [8] and Mott insulating phases [9].

This experiment uses a Bose degenerate gas of 87Rb atoms – a Bose Einstein condensate (BEC) – that is loaded in an optical lattice. This degenerate gas of atoms mimics the role of the Fermi degenerate electron gas in metals, and the wells of the lattice are analogous to the potential wells of ions in metals (see Fig. 2). The larger mass and size of atoms, as compared to electrons, means the relevant quantum dynamics occur more slowly and can thus be directly observed. The only caveat is that the temperature of the gas needs to be close to absolute zero (around a few 10 nK).

**Fig 3:** An optical lattice (a 2D one in this case) can form an egg carton type potential along which the degenerate gas is permitted to travel. Each dimple in the potential is a lattice site, between which the atoms hop. Figure taken from [11].

A BEC loaded in a 1D optical lattice (see Fig. 3) can be in one of two ground state phases: an extended and conducting superfluid phase, or a localized Mott insulating (MI) phase.

A quantum phase transition occurs between these phases as the ratio of tunnelling to onsite interaction is changed. This is usually done by either adjusting the height of the lattice potential, or by adjusting the scattering length of the atoms by means of Feshbach resonance. When interactions dominate, the atoms are pinned to each site and tunnelling is suppressed. As the interactions are reduced, the tunnelling becomes dominant, and the atomic system is now extended. This is an example of a continuous phase transition which occurs in the ground band of the lattice.

**Fig 4:** The MI state in the shaken system is identified by a centrally located broad distribution of the atoms. The π-SF is identified by dual peaks centered around momenta of ±π, indicative of a ground band with negative curvature. The global phase is characterized by the number of atoms around these momenta as a ratio of the total atom number.

Song demonstrates that this phase transition can be made discontinuous by employing a periodic drive to the 1D lattice system. Resonantly shaking the 1D lattice system couples the ground and the first excited band. The larger tunnelling in the first excited band causes an initially prepared Mott insulator to melt into a superfluid state. The negative curvature of the first band causes the condensate to occur at the edges of the Brillouin zone (k = ± π), earning the state the name: π – superfluid (π – SF, see Fig. 4).

**Fig 5:** The measured (left column) phase diagram for two sweeps across the MI to π-SF transition. The first sweep (top) crosses the transition by sweeping the driving frequency across the phase boundary for each driving strength. In the region where the boundary is a discontinuous phase transition the system remains in the initial state despite crossing the boundary. The second sweep (bottom) always crosses the phase boundary in the continuous region such that one always ends up in the final phase. The diagrams on the right column are the accompanying numerical results.

The teams map out the phase diagram of this driven system as a function of the driving parameters: driving strength and the frequency (see Fig. 5). The driven system is described by an effective Hamiltonian. The primary parameters of this Hamiltonian are, detuning from interband resonance, which is controlled by the drive frequency, and the coupling to the drive, which is controlled by the drive strength. The ground state is determined by the competition between these two parameters, in a manner analogous to tunnelling and interaction strength in the static system.

The phase diagram displays the two phases (MI or π-SF) that are separated by a discontinuous and continuous transition depending on the driving strength. The team identifies the discontinuous region by demonstrating the metastability associated with the discontinuous transition.

This experiment represents the first directly observable quantum first order phase transition. By realizing a system with a transition whose character can be tuned to be discontinuous, this study lays the foundations for the creation of metastable states. The unique experimental set up will enable the observation of the quantum decay process of these metastable states.

References:

[1] “Quantum Phase Transitions”, S. Sachdev, Phys. World, 12, 4 (33)
[2] “Some implications of a cosmological phase transition”, T. W. Kibble, Phys. Rep. 67, 183 – 199 (1980)
[3] “Fate of the false vacuum: semiclassical theory.”, S. Coleman, Phys. Rev. D. 15, 2929 (1977)
[4] “Realizing discontinuous quantum phase transitions in a strongly correlated driven optical lattice”, Bo Song et al, Nature Physics, 18, 259–264 (2022)
[5] “Fate of the false vacuum: towards realization with ultra-cold atoms.” ,O. Fialko et al, EPL 110, 56001 (2015)
[6] “The universe on a table top: engineering quantum decay of a relativistic scalar field from a metastable vacuum.”, O. Fialko et al, J. Phys. B: At. Mol. Opt. Phys. 50, 024003 (2017)
[7] “Disorder-assisted assembly of strongly correlated fluids of light”, B. Saxberg et al, Nature 612, 435–441 (2022)
[8] “A cold-atom Fermi-Hubbard anti-ferromagnet”, A. Mazurenko et al, Nature, 545, 462 – 466 (2017)
[9] “Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms”, M. Greiner et al, Nature, 415, 39-44 (2002)
[10] “Interacting Fermionic Atoms in Optical Lattices – A Quantum Simulator for Condensed Matter Physics”, U. Schneider
[11] “Quantum Simulators”, I. Buluta and F. Nori, Science, 326, 5949, 108-111 (2009)

Suppressing relaxation in superconducting qubits by quasiparticle pumping

Authors: Simon Gustavsson, Fei Yan, Gianluigi Catelani, Jonas Bylander, Archana Kamal, Jeffrey Birenbaum, David Hover, Danna Rosenberg, Gabriel Samach, Adam P. Spears, Steven J. Weber, Jonilyn L. Yoder, John Clarke, Andrew J. Kerman, Fumiki Yoshihara, Yasunobu Nakamura, Terry P. Orlando, William D. Oliver

First Author’s Primary Affiliation: Research Laboratory of Electronics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA

Manuscript: Published in Science

Introduction:

Superconducting qubits offer a promising platform for the realization of a functioning quantum computer. There are typically two coherence times relevant to qubit systems, the depolarization time $T_1$ , and the dephasing time, often called $T_2$ . When a qubit undergoes a depolarization event, the qubit emits energy and its state changes, which is also referred to as a “bit flip”. Similarly, when a qubit undergoes a dephasing event, the phase of its quantum state changes, often called a “phase flip”. Unfortunately, quantum systems are always subject to several avenues of decoherence, where the quantum system loses information to its environment. Many schemes to minimize decoherence events exist, dating back to the famous Hahn echo experiment, where refocusing pulses are used to refocus dephasing errors in spin systems (a really nice visual example of this can be seen here). Many of these protocols act as dynamic enhancement of the dephasing time of the quantum system. This paper in Science introduces the first dynamic enhancement of the depolarization time of a superconducting qubit by pumping excitations into a bath of quasiparticles and minimizing their interactions with a superconducting flux qubit.

Experimental Setup and Operating Principle:

This experiment uses two different types of devices, labeled device A and device B. Device A is a flux qubit consisting of four Josephson junctions contained in a superconducting loop (indicated by the smaller red crosses in Fig. 1). A Josephson junction consists of two superconducting islands interrupted by a thin layer of non-superconducting material. In a superconductor, electrons pair together to form ”Cooper pairs” and these Cooper pairs flow through the superconductor without resistance. The physical quantity which describes the state of the effective quantum two level system in this experiment is the direction of the current flowing in the lower superconducting loop. In order to determine the direction of the circulating current, a superconducting quantum interference device (SQUID) acts as a sensitive detector of local magnetic fields and measures the magnetic flux produced by these circulating currents. The SQUID also contains Josephson junctions, which are indicated by the largest red crosses in Fig. 1. This measurement technique involves applying a current to the SQUID, which can be responsible for the generation of quasiparticles, making this device geometry a prime candidate for studying their effects on quantum devices.

Figure 1
Schematic of the first device used in the experiment. The larger red X’s indicate the Josephson junctions which are part the SQUID used for readout, and the smaller X’s indicate the Josephson junctions within the qubit. The qubit states correspond to circulating currents through the lower loop of the figure. The blue circle represents a quasiparticle tunneling across a Josephson junction, which leads to energy decay from the qubit.

In most cases, the quantum system can lose energy to many different decay channels. One primary source of this depolarization is the release of energy from the qubit into quasiparticles, which are unpaired electrons (electrons that are not part of a Cooper pair). It is possible to measure the average number of these quasiparticles by directly measuring the depolarization rate of the system. In order to do this measurement, the authors must give the system some energy to put the qubit into its excited state. By measuring the probability of the qubit remaining in its excited state as a function of time after this excitation pulse, the authors fit the resulting data to the following equation:

$p(t) = e^{\langle n_{qp}\rangle\left(\textrm{exp}\left(-t/ \tilde{T}_{1qp}\right) -1 \right)}e^{-t/T_{1R}}.$

(Equation 1)

The probability of the qubit remaining in the excited state is given as $p(t)$ , the average number of quasiparticles is represented by $\langle n_{qp} \rangle$ , $\tilde{T}_{1qp}$ is the relaxation time provided by a single quasiparticle, and $T_{1R}$ is the decay of the qubit excitation into all channels. By fitting experimental data to Eq. 1, the authors are able to extract the quasiparticle number as a fit parameter, as well as distinguish the difference between qubit decays into quasiparticles versus decays into other channels. A measurement of the qubit lifetime and fit to Eqn. 1 is shown in Fig. 2. The authors find that the average quasiparticle number in this measurement is $\langle n_{qp} \rangle = 2.5$ , the decay induced by a single quasiparticle is $T_{1qp} = 23 \mu s$ , and decay to all other channels is given by $T_{1R} = 55 \mu~s$ .

Figure 2
A measurement of qubit energy relaxation. The dots represent the measured data and the black line is a fit to Eqn. 1. The fit parameters are given in the box in the upper right hand corner. From the fit, we see that there is an average population of 2.5 quasiparticles.

Although the presence of quasiparticles can reduce the lifetime of the qubit, this idea can be used advantageously to extend the lifetime of the qubit by using special control schemes. When the qubit emits energy into the bath of quasiparticles, the qubit loses energy $\hbar \omega_q$ , where $\omega_q$ is the resonant frequency of the qubit. In turn, the bath of quasiparticles must gain the same amount of energy, $\hbar \omega_q$ . This increase of quasiparticle energy leads to an increase of the velocity of the quasiparticle and ”pushes” it away from the qubit so that it can no longer cause depolarization of the qubit! The authors take advantage of this mechanism by exciting the qubit a number of times with a pulse of microwaves (often times these excitations are called $\pi$ pulses since they rotate the qubit state by $\pi$ radians on a unit sphere, see this page for a nice visual example!). By waiting for an amount of time $30 \mu~s$ between $\pi$ pulses, any decay of the qubit during this time is most likely into quasiparticles, since the authors measure $\tilde{T}_{1qp} < T_{1R}$ (see. Fig. 2). By applying many of these pulses and continuously monitoring the qubit population, the authors see that the decay of the qubit excited state slows down with each consecutive $\pi$ pulse! The results for up to four pulses can be seen in Fig. 3.

Figure 3
Measurement of qubit population with consecutive $\pi$ pulses. It is clear that the qubit decay ”slows down” with each consecutive pulse, indicating that there are fewer quasiparticles causing decay with each measurement.

Figure 3
Measurement of qubit population with consecutive $\pi$ pulses. It is clear that the qubit decay ”slows down” with each consecutive pulse, indicating that there are fewer quasiparticles causing decay with each measurement.

In order to fully investigate the impact of these quasiparticle pumping pulses, the authors extend this process to include up to 40 $\pi$ pulses under the same conditions. The authors measure the qubit decay time (defined to be the amount of time it takes for the signal to decay by a factor of 1/e) as a function of the number of refocusing pulses with a time interval of $10~\mu s$ between pumping pulses. After the last pulse, the authors measure the probability of the qubit being in its excited state as a function of time after the last pulse (a similar measurement to that in Fig. 3, only this time with the sequence of pumping pulses added to the beginning of the measurement protocol). The authors find that the qubit decay time increases with the number of pumping pulses, implying that each pulse is actually pushing these quasiparticles away from the qubit. The results are shown in in Fig. 4.

Figure 4
(a) Pulse sequence which describes the quasiparticle pumping mechanism. Consecutive $\pi$ pulses are applied to the qubit with some variable time $\Delta$ T $= 30\mu$ s, finally the qubit is excited into its excited state and its decay is measured. (b) Results of the measured qubit decay as a function of the number of pump pulses. The observed qubit decay time increases with increasing pulse number. (c) The measured quasiparticle population, which is shown to initially decrease with pulses number before saturating near $\langle n_{qp} \rangle = 0.5$ . (d) Measured induced decay per quasiparticle.

Figure 4
(a) Pulse sequence which describes the quasiparticle pumping mechanism. Consecutive $\pi$ pulses are applied to the qubit with some variable time $\Delta$ T $= 30\mu$ s, finally the qubit is excited into its excited state and its decay is measured. (b) Results of the measured qubit decay as a function of the number of pump pulses. The observed qubit decay time increases with increasing pulse number. (c) The measured quasiparticle population, which is shown to initially decrease with pulses number before saturating near $\langle n_{qp} \rangle = 0.5$ . (d) Measured induced decay per quasiparticle.

In addition, the authors extract the mean quasiparticle number as a function of pulse number, and find that the quasiparticle number decreases with each pulse until the quasiparticle number saturates near $\langle n_{qp} \rangle \sim 0.5$ . The authors also find that the lifetime of the qubit due to a single quasiparticle decreases with pulse number, which is somewhat surprising, since we would expect that each individual quasiparticle would impact the qubit lifetime in the same way. This feature is understood because as the number of pulses is increased, the quasiparticles near the qubit generally have larger energy and will actually give some energy back to the qubit as well as taking energy away from it. These competing factors may actually lead to a reduction of $\tilde{T}_{1qp}$ .

To verify that this pumping scheme works for different types of systems, the authors utilize the same experimental protocol on another type of qubit, called a C-shunt flux qubit (see Fig. 5a for an image of the device), which is less sensitive to quasiparticles. The authors use the same method of applying $\pi$ pulses to the qubit to transfer energy to the quasiparticle bath, and their results are shown in Fig. 5.

Figure 5
(a) New device geometry which is less sensitive to quasiparticle tunneling. Because the readout mechanism doesn’t involve sourcing a current near the Josephson junctions which constitute the qubit, one might expect quasiparticles to be less important for qubit relaxation. (b) Measured qubit decay with and without quasiparticle pumping pulses. As seen from the fit, the qubit decay time increases by approximately a factor of two.

As seen in Fig. 5, even though the device is less sensitive to quasiparticles, when the authors use 5 pumping pulses, the average number of quasiparticles decreases by a factor of two and the qubit lifetime is increased by a factor of two!

Finally, in order to investigate the consistency of this pumping scheme, the authors continuously monitor the qubit decay with and without pumping pulses over 9 hours. In this data set, the experimental setup is in a configuration where the qubit decay is well described only by a single exponentially decaying function. Even so, the authors still find that the qubit decay time is increased when the pumping scheme is applied (see Fig. 6a). In the absence of quasiparticle pumping, the authors find large fluctuations in the decay time of the qubit, which leads to low signal-to-noise ratio in the data (see Fig. 6b, left panel, and Fig. 6c). When the pumping sequence is applied to the system, the measurements become much more stable, with fluctuations in the signal dominated by the noise added by the amplifiers in the system (see Fig. 6c).

Figure 6
(a) Measured qubit decay approximately one week after the data in the previous figure. In this data set, the decay is well described by only a single exponential function, yet the presence of pumping pulses is still found to increase the decay constant of the qubit lifetime. (b) Measurements of the qubit decay time as a function of time without (left) and with (right) quasiparticle pumping pulses. The pumping sequence significantly reduces the fluctuations in time of the measured data. (c) Standard deviation as a function of time of the data in (b). It is clear that the pumping pulses keep the fluctuations at a constant value in time, while in the absence of pumping pulses, the fluctuations are much larger at short delay times.

Conclusions:

In conclusion, the authors have introduced a new type of control scheme over superconducting qubits which gives energy to a local bath of quasiparticles near the qubit, and therefore ”pushes” them away from the qubit. As the quasiparticles diffuse away from the qubit, the qubit loses energy into the quasiparticle bath less frequently and therefore the qubit decay time is increased. Additionally, the authors verify that this scheme improves the qubit decay time across two different types of device geometries and find that it decreases fluctuations in the measured signal from the system. These experiments allow the authors not only to learn about the quasiparticle population in their devices, but also simultaneously improve the device performance. Outside of the field of quantum error correction, this work is the first demonstration of a dynamic enhancement of the qubit depolarization time $T_1$ .

Disipación Controlada con Cúbits Superconductores

Por Joe Kitzman

Este post fue patrocinado por Tabor Electronics. Para mantenerte al día con los productos y aplicaciones de Tabor, únete a su comunidad en LinkedIn y suscríbete a su boletín informativo.

Autores: P.M. Harrington, M. Naghiloo, D. Tan, K.W. Murch

Afiliación Primaria del Primer Autor: Departamento de Física, Universidad de Washington, Saint Louis, Missouri 63130, USA

Original: Publicado en Physical Review A

Introducción

Los sistemas cuánticos son generalmente muy sensibles y al interaccionar con el entorno, sus propiedades cuánticas pueden perder coherencia. Esto esencialmente hace que un determinado sistema cuántico se disipe en un comportamiento puramente clásico. No obstante, en ciertos contextos es posible usar esta disipación de una manera controlada para incrementar el control sobre los sistemas cuánticos. Algunos ejemplos de esta disipación controlada incluyen el enfriamiento de átomos por láser, el enfriamiento de osciladores mecánicos a bajas frecuencias y el control de los circuitos cuánticos. En esta reciente publicación [1], los autores son capaces de demostrar la estabilización de los estados de superposición en un cúbit superconductor usando un canal de pérdidas de cristal fotónico hecho a medida. Considerando cómo el cristal fotónico induce pérdidas en el sistema, los autores proporcionan un enfoque con ecuación maestra que explica cómo la combinación de un impulso especializado aplicado al cúbit, además de la disipación dada por el cristal fotónico, permite un control preciso del estado del cúbit por tiempos mucho mayores que los tiempos de coherencia estándar de un cúbit.

Detalles Experimentales

Este experimento consiste en un cúbit superconductor cuyo momento dipolar se acopla al campo eléctrico dentro de una cavidad de guía de ondas tridimensional. En este experimento, el rol de la cavidad de guía de ondas es facilitar el control por microondas del cúbit así como leer el estado del cúbit. El cúbit superconductor consiste en dos uniones de Josephson en paralelo, formando un dispositivo interferométrico cuántico superconductor (a menudo conocido como “SQUID” por sus siglas en inglés: superconducting quantum interference device). Esto permite a los autores cambiar la frecuencia de resonancia del cúbit haciendo pasar un campo magnético externo a través de la espira del SQUID. En la salida de la cavidad de guía de ondas, los autores conectan un cristal fotónico al circuito. Este cristal fotónico está hecho de un cable coaxial usual que está mecánicamente deformado de una manera concreta para cambiar su impedancia. El resultado de la impedancia que varía con el espacio en el cable causa la apertura de una banda prohibida – llegando a energías fotónicas (o frecuencias) donde la densidad fotónica de los estados es cero (ver Fig. 1 para un esquema del montaje experimental). Cambiando la densidad fotónica de los estados en función de la energía, el decaimiento del cúbit también cambiará en función de la frecuencia.

Figura 1
Izquierda: Esquema del sistema experimental. El cúbit superconductor se monta en una cavidad de cobre que se usa para controlar y leer el estado del cúbit. Haciendo pasar corriente a través del cable superconductor enroscado alrededor de la cavidad se genera un campo magnético perpendicular al sustrato que contiene al cúbit, permitiendo a los autores sintonizar la frecuencia de resonancia del cúbit. El cristal fotónico se conecta al puerto de salida de la cavidad, cambiando la densidad de los estados sobre los que puede decaer el cúbit. Derecha: Medidas a temperatura ambiente de la reflexión del cristal fotónico. En la banda de corte (de 5.5 – 6.4 GHz) la mayor parte de la señal enviada al cristal fotónico se refleja, verificando que hay una baja densidad de estados a esas frecuencias. Por encima de 6.4 GHz, la banda fotónica prohibida se estrecha y los fotones se pueden transmitir a través del cristal fotónico.

Tasas de Decaimiento del Cúbit

Para medir la tasa de decaimiento del cúbit, los autores primero llevan el cúbit a su estado excitado aplicando un pulso de energía al sistema que es resonante con el cúbit. Luego, miden la probabilidad de que el cúbit permanezca en su estado excitado en función del tiempo después de haber aplicado el pulso. Ajustando la probabilidad medida a un decaimiento exponencial y extrayendo la constante de decaimiento, se puede determinar la tasa de decaimiento del cúbit. La frecuencia de resonancia del cúbit se ajusta luego cambiando el flujo magnético externo que circula por la espira del SQUID y midiendo la tasa de decaimiento del cúbit en función de la frecuencia del cúbit para investigar el impacto del cristal fotónico sobre la vida media del cúbit. La tasa de decaimiento total del cúbit se puede expresar como

$\gamma_1 = \gamma_d + \rho(\omega_q)(g/\Delta_q)^2 \kappa.$

En la Ec. 1, $\gamma_1$ es la tasa de decaimiento medida del cúbit, $\kappa/2\pi = 18~\textrm{MHz}$ es el ancho de banda de la cavidad de microondas, $g/(2\pi) = 200~\textrm{MHz}$ es la fuerza de acoplamiento entre el cúbit y la cavidad, $\Delta_q = \omega_c - \omega_q$ es la diferencia en frecuencia de resonancia entre el cúbit y la cavidad, $\rho(\omega_q)$ es la densidad de estados del cristal fotónico a la frecuencia del cúbit, y $\gamma_d$ representa el decaimiento del cúbit en canales de disipación aparte del cristal fotónico. Midiendo la tasa de decaimiento total del cúbit para varios valores de $\omega_q$ , ¡debería ser posible extraer información acerca de la densidad de estados del cristal fotónico! Ver Fig. 2 a continuación para la medida resultante.

Figura 2
Medida de las tasas de decaimiento del cúbit sobre un rango amplio de frecuencias. Dado que la pérdida del cúbit varía rápidamente con la frecuencia del cúbit, llevando el flujo de polarización al punto donde la derivada de la pérdida del cúbit es grande, las bandas laterales del triplete de Mollow pueden muestrear frecuencias tanto con muy altas como con muy bajas pérdidas. Midiendo las frecuencias generalizadas de Rabi a lo largo de los mismos valores de frecuencia del cúbit, los autores verifican la variable de acoplamiento del cúbit con el cristal fotónico.

Dinámica y Emisión de un Cúbit Controlado

Después de verificar que la densidad de estados en el cristal fotónico puede modificar la tasa de decaimiento del cúbit, los autores ahora consideran más cuidadosamente cómo emite el cúbit energía realmente. Específicamente, se considera un fuerte impulso aplicado con amplitud $\Omega$ que es desintonizado de la energía del cúbit una cantidad $\Delta = \omega_d - \omega_q$ , donde $\omega_d$ es la frecuencia del impulso y $\omega_q$ es la energía del cúbit. Si la amplitud del impulso es mucho mayor que la tasa de pérdida del cúbit, el cúbit emitirá energía a tres frecuencias diferentes $\omega_d$ y $\omega_d~\pm~\Omega_R$ , donde $\Omega_R = \sqrt{\Omega^2 + \Delta^2}$ se conoce como frecuencia de Rabi generalizada. Este espectro de emisión se llama triplete de Mollow [2]. Ver Fig. 3 para un esquema de emisión del triplete de Mollow.

Figura 3
Esquema que representa la emisión del sistema de dos niveles controlado. Bajo la presencia de un impulso fuerte, el cúbit emite radiación a frecuencias correspondientes a la frecuencia del impulso $\omega_d$ así como a frecuencias $\omega_d \pm \Omega_R$ . Debido al espectro de pérdidas modificado, el área de una banda lateral puede disminuir, indicando que el cúbit emitirá radiación a esta frecuencia en menor medida que la otra banda lateral. Arriba a la derecha: bajo la presencia del impulso, el eje de cuantización del cúbit también rota, lo cual cambia los estados del cúbit que se pueden preparar / estabilizar.

Figura 3
Esquema que representa la emisión del sistema de dos niveles controlado. Bajo la presencia de un impulso fuerte, el cúbit emite radiación a frecuencias correspondientes a la frecuencia del impulso $\omega_d$ así como a frecuencias $\omega_d \pm \Omega_R$ . Debido al espectro de pérdidas modificado, el área de una banda lateral puede disminuir, indicando que el cúbit emitirá radiación a esta frecuencia en menor medida que la otra banda lateral. Arriba a la derecha: bajo la presencia del impulso, el eje de cuantización del cúbit también rota, lo cual cambia los estados del cúbit que se pueden preparar / estabilizar.

Dado que los autores han observado que el cristal fotónico modifica la tasa de pérdida del cúbit en una escala de energía comparable a los valores experimentales accesibles de $\Omega_R$ , es posible que una de las bandas laterales del triplete de Mollow experimente una tasa de pérdidas grande mientras que la otra banda lateral experimenta una tasa baja.

Lo siguiente a considerar es cómo afecta la presencia de un impulso aplicado al espectro de energía del cúbit. En un sistema de referencia en rotación con la frecuencia del impulso, el hamiltoniano del cúbit viene dado por

$H_q = \frac{\Delta}{2}\sigma_z + \frac{\Omega}{2}\sigma_x,$

donde $\sigma_z$ y $\sigma_x$ son matrices de Pauli. Dado que este hamiltoniano no es diagonal, es conveniente rotar la base de manera que el hamiltoniano se pueda escribir de la forma

$\tilde{H}_q = \frac{\Omega_R}{2}\tilde{\sigma}_z,$

donde la matriz de Pauli Z rotada puede expresarse como $\tilde{\sigma}_z = \sin{2\theta}\sigma_x - \cos{2\theta}\sigma_z$ y el ángulo de rotación se define como $\tan{2\theta} = -\Omega/\Delta$ con $0<\theta<\pi/2$ . Dado que hemos escrito el hamiltoniano en una base rotada, debemos considerar también cómo rotan los nuevos autoestados del sistema con respecto a los autoestados originales, que llamaremos $|g\rangle$ y $|e\rangle$ para los estados fundamental y excitado, respectivamente.

$|\tilde{g}\rangle = \cos{\theta}|g\rangle - \sin{\theta}|e\rangle$

$|\tilde{e}\rangle = \sin{\theta}|g\rangle + \cos{\theta}|e\rangle$

Llegados a este punto, ¡probablemente sea conveniente considerar un ejemplo útil! En el caso de un impulso resonante, $\Delta = 0$ , que inmediatamente nos informa de que $\theta = 45^{\circ}$ , por lo que podemos reescribir los autoestados rotados del sistema como $|\tilde{g}\rangle = \frac{1}{\sqrt{2}}(|g\rangle - |e\rangle) \equiv |-x\rangle$ y $|\tilde{e}\rangle = \frac{1}{\sqrt{2}}(|g\rangle + |e\rangle) \equiv |+x\rangle$ , los cuales tienen la propiedad especial de que $\sigma_x|\pm x\rangle = \pm 1 |\pm x\rangle$ . Dado que el estado $|-x\rangle$ tiene una energía menor, emitirá energía correspondiente a la banda lateral de menor energía del triplete de Mollow y viceversa para el estado $|+x\rangle$ . Si la pérdida del cúbit es muy diferente para cualquiera de estos estados, ¡fomentará el decaimiento hacia los estados $|-x\rangle$ o $|+x\rangle$ ! Específicamente, si el cúbit está a una frecuencia de resonancia cercana a 6.4766 GHz (ver Fig. 2), el estado de mayor energía (correspondiente a $|+x\rangle$ en este ejemplo) tiene una tasa de pérdida menor, por lo que deberíamos esperar que mientras el impulso esté activo, ¡el cúbit preferentemente decaerá hacia este estado! ¡Esto significa que el valor esperado $\langle \sigma_x \rangle$ tenderá a +1 en este supuesto! En el caso de un espectro de pérdidas uniforme, no habría un decaimiento preferido para el cúbit y sería de esperar que todos los valores esperados decayeran a cero.

La Ecuación Maestra de Lindblad

En presencia del impulso combinado y la disipación sufrida por el cúbit, la dinámica de la matriz de densidad reducida que describe el cúbit puede ser expresada de acuerdo a la ecuación maestra de Lindblad [3]:

$\dot{\rho} = i[\rho,H] + \gamma_0 \cos{(\theta)}\sin{(\theta)}\mathcal{D}[\tilde{\sigma}_z]\rho + \gamma_{-} \sin{^4\left(\theta\right)} \mathcal{D}[\tilde{\sigma}_{+}\rho + \gamma_{+}\cos{^4\left(\theta\right)} \mathcal{D}[\tilde{\sigma}_{-}]\rho.$

Aquí, $\rho$ es la matriz de densidad reducida para el cúbit, el superoperador de disipación también se introduce como $\mathcal{D}[A]\rho = \left( 2 A \rho A^{\dagger} - A^{\dagger}A\rho - \rho A^{\dagger}A\right)/2$ . La tasa $\gamma_0$ representa un desfase del cúbit en la base rotada de $\theta$ , que se acopla al operador $\tilde{\sigma}_z$ y las transiciones entre autoestados en la base rotada son controlados por los operadores de “salto” $\tilde{\sigma}_{\pm}$ , que están relacionados con las tasas $\gamma_{\mp}$ . Similar al ejemplo anterior, si el cristal fotónico modifica la pérdida del cúbit tal que $\gamma_{\pm} \gg \gamma_{\mp}$ , el autoestado del sistema de referencia en rotación correspondiente se estabilizará.

Resultados experimentales

Para verificar que los autores pueden usar la combinación de impulsos y disipación para preparar y estabilizar estados de cúbits, implementan el siguiente protocolo de bath engineering. Primero, se lleva el flujo de polarización del cúbit a la frecuencia de resonancia de 6.4766 GHz (como en nuestro ejemplo). Después, se aplica un impulso coherente al sistema durante casi $16~\mu s$ (¡que es mucho más largo que el tiempo de coherencia del cúbit en ausencia del impulso!). Durante este tiempo, el cúbit debería decaer preferiblemente a un autoestado del sistema rotado si las bandas laterales del triplete de Mollow tienen pesos diferentes. Una vez se corta el impulso, se mide el valor esperado $\langle \sigma_x \rangle$ para varias combinaciones de parámetros del impulso. Los resultados se muestran a continuación también en la Fig. 4 como comparaciones con los resultados numéricos a la ecuación maestra, los autores no solo ven que los valores esperados del cúbit no decaen a 0, ¡sino que hay una concordancia fantástica entre la teoría y el experimento!

Figura 4
(a) Medida de $\langle \sigma_x \rangle$ mientras que los parámetros del impulso van cambiando. Para ciertos parámetros del impulso, el valor de $\langle \sigma_x \rangle$ es negativo. Así como van cambiando los parámetros del impulso, el sistema pasa por una región de “cero coherencia”, donde el protocolo de *bath engineering* ya no funciona antes de estabilizar $\langle \sigma_x \rangle$ a valores positivos . (b) Soluciones numéricas a la ecuación maestra bajo los mismos parámetros de impulso que (a). Los autores observan una excelente correspondencia entre los experimentos y las soluciones numéricas. (c) Comparación de las líneas de corte horizontales de (a,b). Los autores observan una concordancia entre los valores medidos (puntos) y los valores simulados (líneas) cuando se consideran todos los valores esperados para el estado del cúbit ( $\langle \sigma_{x,y,z} \rangle$ ).

Figura 4
(a) Medida de $\langle \sigma_x \rangle$ mientras que los parámetros del impulso van cambiando. Para ciertos parámetros del impulso, el valor de $\langle \sigma_x \rangle$ es negativo. Así como van cambiando los parámetros del impulso, el sistema pasa por una región de “cero coherencia”, donde el protocolo de *bath engineering* ya no funciona antes de estabilizar $\langle \sigma_x \rangle$ a valores positivos . (b) Soluciones numéricas a la ecuación maestra bajo los mismos parámetros de impulso que (a). Los autores observan una excelente correspondencia entre los experimentos y las soluciones numéricas. (c) Comparación de las líneas de corte horizontales de (a,b). Los autores observan una concordancia entre los valores medidos (puntos) y los valores simulados (líneas) cuando se consideran todos los valores esperados para el estado del cúbit ( $\langle \sigma_{x,y,z} \rangle$ ).

Conclusión

En conclusión, los autores son capaces de demostrar la fabricación de un cable coaxial con impedancia que varía en el espacio que actúa como un cristal fotónico y a cambio controlan el espectro de pérdidas de un cúbit superconductor. Los autores luego hacen uso de este espectro de emisión modificado en el contexto de la ecuación maestra para preparar y estabilizar estados no triviales del cúbit por tiempos mucho mayores que los tiempos de coherencia del cúbit.

Referencias

[1] P. M. Harrington, M. Naghiloo, D. Tan, and K. W. Murch, Bath engineering of a fluorescing artificial atom with a photonic crystal, Phys. Rev. A 99, 052126 (2019)

[2] B. R. Mollow, Power spectrum of light scattered by two-level systems, Phys. Rev. 188, 1969 (1969)

[3] G. Lindblad, On the generators of quantum dynamical semigroups, Communications in Mathematical Physics 48, 119 (1976).

What can quantum information tell us about the foundations of statistical mechanics?

By Mauro E.S. Morales

Title: Entanglement and the foundations of statistical mechanics

Authors: Sandu Popescu^1,2, Anthony J. Short¹, Andreas Winter³.

Institutions: ¹H. H. Wills Physics Laboratory, University of Bristol, Tyndall Avenue, Bristol BS8 1TL, UK

²Hewlett-Packard Laboratories, Stoke Gifford, Bristol BS12 6QZ, UK

³Department of Mathematics, University of Bristol, University Walk, Bristol BS8 1TW, UK

Manuscript: Published in Nature [1], Open Access on arXiv [2]

It is sometimes easy to forget, that in addition to the impact it has had on the development of new technologies, the ongoing development of quantum information theory has had implications on the foundations of Physics itself. In fact, based on insights from quantum information, in [1] the authors argue for re-framing a fundamental principle that lies is at the very basis of statistical mechanics, namely the equal probability postulate.

The concept of a thermodynamic “equilibrium” is central to classical statistical mechanics. In such an equilibrium, one can assume that there are no macroscopic changes in a given system. Consider a box full of solid particles inside, and take this box to be connected to a heat bath of temperature $T$ and isolated from everything else. For a given temperature, we know that the probability that the system is in a state with energy $E_i$ is given by

$P(E_i)=\frac{1}{Z}e^{-E_i /kT} ,$

where $Z$ is the well-known partition function, which roughly tells us how many different ways one can partition a system into subsystems having the same energy, and $k$ is the Boltzmann constant which relates absolute temperature to the kinetic energy of each microscopic particle in any given system.

A key assumption in this is that all possible states of the “total system”, which encapsulates the box and the bath, have equal probability. This assignment of probabilities to each energy is known as the canonical ensemble. Physicists also work with other types of ensembles, for instance, the micro-canonical ensemble, where the total energy is fixed and all states have equal probability. It is important to stress that this is an assumption on the total system, not something that is proven from other postulates. In other words, we postulate this a priori.

A general canonical principle

In [1], the authors propose a way to derive probabilities assigned by the canonical ensemble by explicitly considering quantum systems. In fact, their methods prove a more general canonical principle than the classical one, and we shall elaborate on this general principle further.

First, let us consider a large isolated quantum system $R$ described by a Hilbert space $\mathcal{H}_R$ which is decomposed into a system $S$ with Hilbert space $\mathcal{H}_S$ and an environment $E$ with Hilbert space $\mathcal{H}_E$ . In principle $\mathcal{H}_R$ could be described by $\mathcal{H}_S\otimes \mathcal{H}_E$ , but we can consider restrictions over the space as shown in the picture below.

This restriction would make the space $R$ smaller and would be analogous to the system presented in the introduction with a fixed temperature $T$ . In a quantum setting, such restrictions are described by considering constraints on the possible joint states of system $S$ and $E$ . We note that such restrictions need not be related solely to temperature, it can in fact be any type of constraint whatsoever on the total system, a feature that will turn out to be important for the generality of the proof.

We can consider as in classical thermodynamics, the state that gives equal probability to all states in $\mathcal{H}_R$ , which can be represented using the identity matrix. This state gives equal probability to all states of $R$ , assuming that $R$ is in this state is akin to the assumption in the combined box/bath example in the introduction.

In this case, the canonical state would be obtained by tracing out the degrees of freedom from the bath. We denote this state as $\Omega_S$ . If we had taken the system $R$ as the box/bath combined with the restriction of the temperature $T$ , then $\Omega_S$ would correspond to the Gibbs state, which describes an equilibrium probability distribution that remains invariant under any future evolution of the system, with the probabilities given in the introduction. So far, we have just rewritten everything in the language of quantum mechanics but the authors take a step further. It’s important to remark that we could have taken any other restriction for $\mathcal{H}_R$ and the canonical state would be different from the canonical thermal canonical state defined earlier in the introduction.

What if the state of $R$ is not the identity?

If the state of $R$ corresponds instead to some state $|\phi\rangle \langle \phi |$ and defines the state of the system $S$ as $\rho_S=Tr_{E}\left( |\phi\rangle \langle \phi |\right)$ , then the authors show that $\rho_S$ is close to the state $\Omega_S$ for almost all possible states $|\phi\rangle \langle \phi |$ . This implies that there is no need to assume equal probability for all states since, as we will see, most of the states in system $R$ will give the correct canonical state in $S$ .

In quantum information, we can measure how close two states are from each other using the so-called trace distance. We will denote the distance between $\rho_S$ and $\Omega_S$ as $D(\rho_S,\Omega_S)$ .

This distance represents the maximal difference between the two states in the difference of obtaining any measurement. In other words, the trace distance tells us how hard is to tell apart $\rho_S$ and $\Omega_S$ apart under measurements (the greater the distance, the harder to tell apart).

Distance between density matrices is defined by D

To understand what the authors prove let’s set some notation. Let $\rho_S (\phi)=Tr_{E}\left( |\phi\rangle \langle \phi |\right)$ be the state obtained by tracing out the environment and define the set of states at a distance of the canonical state equal or greater to $\eta$ as $\mathcal{S}$ . The radius defined by $\eta$ is shown below.

Note that $\mathcal{S}$ is a set in the Hilbert space $\mathcal{H}_R$ (different from the one pictured above, which is the space of density matrices). We picture below the set $\mathcal{S}$

The set $\mathcal{S}$ fills a volume in the Hilbert space, we denote the fraction of states at distance equal or greater to $\eta$ of the canonical state as

$\frac{V\left(\mathcal{S}\right)}{V\left(\mathcal{H}_R\right)}$

where $V(\cdot)$ refers to the “volume” of the set in the argument. Another way of interpreting this ration is as the probability of picking a random state $|\phi\rangle$ such that the distance of $\rho_S$ to the canonical state is equal or greater to $\eta$ .

What the authors prove rigorously is that this probability gets smaller (in fact exponentially smaller) as $\eta$ grows. More precisely they prove that for $\epsilon>0$ we have that

$\frac{V\left(\mathcal{S}\right)}{V\left(\mathcal{H}_R\right)}\leq \eta'$

with $\eta\approx\epsilon$ and $\eta'=4 \exp(-Cd_R \epsilon^2)$ .

Note that as $\epsilon$ grows, the probability, of picking a state such that the distance is big enough, decays exponentially.

We won’t go into the full intricacies of the proof for this statement, but we will mention that a key ingredient is Levy’s lemma (for those curious about this Lemma, see [2]). This lemma has in fact seen use in other areas of quantum information. Those familiar with variational quantum algorithms may have heard of barren plateaus, which limit the trainability of variational circuits [3]. Levy’s lemma is a key ingredient in proving that under certain conditions barren plateaus become inevitable when training these quantum circuits.

References

[1] Popescu, S., Short, A. & Winter, A. Entanglement and the foundations of statistical mechanics. Nature Phys 2, 754–758 (2006). https://doi.org/10.1038/nphys444

[2] Popescu, S., Short, A. & Winter, A. The foundations of statistical mechanics from entanglement: Individual states vs. averages. arXiv:0511225 [quant-ph], Oct. 2006.

[3] McClean, J.R., Boixo, S., Smelyanskiy, V.N. et al. Barren plateaus in quantum neural network training landscapes. Nat Commun 9, 4812 (2018). https://doi.org/10.1038/s41467-018-07090-4

Control cuántico del movimiento

Por Akash Dixit

Título: Preparación de estados cuánticos, tomografía y entrelazamiento de osciladores mecánicos

Autores: E. Alex Wollack, Agnetta Y. Cleland, Rachel G. Gruenke, Zhaoyou
Wang, Patricio Arrangoiz-Arriola, y Amir H. Safavi-Naeini

Institución: Departamento de Física Aplicada y Laboratorio de Ginzton, Universidad de Stanford 348 Via Pueblo Mall, Stanford, California 94305, USA

Original: Publicado en Nature [1], Acceso libre en arXiv

Introducción
El campo de las ciencias de la información cuántica contiene multitud de diferentes tecnologías, incluyendo átomos, espines y defectos en los centros de diamante. Este trabajo se centra en dos tecnologías emergentes: circuitos superconductores y osciladores mecánicos. Cada sistema tiene sus ventajas, pero no es obvio que ninguna sea la mejor plataforma para construir un ordenador cuántico, desarrollar sensores cuánticos o facilitar la comunicación cuántica. Para alcanzar estos objetivos es necesario desarrollar un sistema cuántico híbrido que pueda utilizar los puntos fuertes de diversas tecnologías cuánticas.

En este trabajo, los autores demuestran la posibilidad de acoplar cúbits superconductores a movimiento mecánico. Esto establece los cimientos para un sistema cuántico híbrido que pueda aprovechar lo mejor de los dos sistemas. El cúbit es personalizable y fácil de comunicarse con él, haciéndolo ideal para la inicialización y caracterización del estado. Los modos mecánicos se fabrican con escasa huella espacial y tienen tiempos de vida largos, haciendo posible escalarlos a sistemas más grandes y mantener la información cuántica durante largos períodos de tiempo. A continuación, describiré cómo los autores usan estos acoplamientos entre los dos sistemas tanto para preparar como para medir los estados de movimiento mecánico usando el cúbit. Primeramente, describo el sistema cuidadosamente diseñado que acopla un cúbit a dos osciladores mecánicos. Después, hablo de los dos modos de operación, donde el cúbit es usado tanto para preparar estados de movimiento mecánico como para medir el estado cuántico del modo mecánico. Finalmente, muestro cómo los autores usan el cúbit como un intermediario para preparar estados mecánicamente entrelazados entre los dos osciladores.

Mecanismo

El dispositivo usado en este trabajo consiste en dos osciladores mecánicos y un cúbit superconductor. Los osciladores mecánicos se fabrican en una lámina delgada de niobato de litio (LiNbO₃). Estos osciladores se forman provocando un defecto en una estructura periódica del material, llamado cristal fonónico. El defecto es un desajuste en la periodicidad de la estructura y confina el movimiento mecánico, impidiendo la radiación acústica y permitiendo períodos de integridad largos. Al igual que ocurre con la radiación electromagnética, el movimiento mecánico puede ser cuantizado. Los quantum del movimiento mecánico se llaman fonones y el oscilador mecánico puede ser caracterizado como un oscilador armónico con niveles de energía equiespaciados. El cúbit se hace fabricando un oscilador $LC$ con materiales superconductores. El elemento clave de este circuito es la unión de Josephson, que está hecha de óxido de aluminio intercalado entre capas de aluminio superconductor. La unión actúa como un inductor no lineal que modifica la distancia entre los niveles de energía del oscilador $LC$ . Los niveles de energía del oscilador $LC$ usual (que es un oscilador armónico) están equiespaciados, lo que significa que la energía de transición entre dos niveles cualesquiera es la misma. Sin embargo, con el inductor no lineal en el circuito, ya no hay niveles de energía equiespaciados, haciendo posible distinguir los dos niveles de menor energía del sistema, el fundamental ( $\left| g \right\rangle$ ) y el excitado ( $\left| e \right\rangle$ ). Los dos niveles forman un bit cuántico (cúbit). El cúbit está diseñado para que se pueda ajustar su frecuencia poniendo dos uniones de Josephson en paralelo. Aplicando un campo magnético mediante un cable que lleve corriente, se produce un flujo magnético a través de la espira que permite cambiar la frecuencia del cúbit.

El cúbit y los osciladores mecánicos se fabrican en chips separados que se colocan a una distancia $\sim \mu m$ . Para acoplar el cúbit con los osciladores mecánicos, los autores usan la piezoelectricidad de la lámina de niobato de litio. El movimiento mecánico de este material produce una acumulación de carga eléctrica sobre los paneles de aluminio situados en ambos chips, que están diseñados para ser el elemento capacitivo del cúbit. El cúbit capacitor se carga con el movimiento de los osciladores mecánicos, garantizando que los dos sistemas están conectados.

Inicializando un estado mecánico
Los autores diseñan el cúbit para que interaccione de dos maneras diferentes con los osciladores mecánicos. En el primer modo, el cúbit está sintonizado para entrar en resonancia con un oscilador mecánico en concreto ( $\omega_q = \omega_1, \omega_2$ ). Nótese que las frecuencias mecánicas de los dos osciladores son diferentes, así que el cúbit sólo puede estar en resonancia con una a la vez. Esto permite el intercambio directo de energía entre el cúbit y cada oscilador a una tasa relacionada con el acoplamiento capacitivo entre los dos, $g_1 = 2 \pi \times$ 9.5 MHz, $g_2 = 2 \pi \times$ 10.5 MHz. El hamiltoniano que describe la interacción entre el cúbit y el oscilador mecánico en resonancia es la interacción de Jaynes-Cummings:

$\mathcal{H}_{\mathrm{on}} = g(a^{\dagger} \sigma^{-} + a \sigma^{+})$
[Ecuación 1].

$a^{\dagger}, a$ y $\sigma^{+}, \sigma^{-}$ son los operadores creación y destrucción para el oscilador mecánico y el cúbit, respectivamente. Cuando están en resonancia, el cúbit y el oscilador mecánico intercambian sus respectivos estados en un tiempo de $\pi/g \sim$ 24-26 $ns$ dependiendo del oscilador en cuestión.

Figura 2: **Intercambio de estados entre cúbit y oscilador.** El cúbit (Q) se inicializa en el estado excitado. Una vez el cúbit se lleva a resonancia con el oscilador mecánico, los dos intercambian sus estados coherentemente. Esto significa que el estado del sistema oscila entre $\left| 0,e \right\rangle$ y $\left| 1,g \right\rangle$ , donde $\left| m,g \right\rangle$ representa el estado de la mecánica y del cúbit. Entre un intercambio completo, el cúbit y los osciladores mecánicos están entrelazados con función de estado $\left| 1,g \right\rangle + \left| 0,e \right\rangle$ .

Figura 2: **Intercambio de estados entre cúbit y oscilador.** El cúbit (Q) se inicializa en el estado excitado. Una vez el cúbit se lleva a resonancia con el oscilador mecánico, los dos intercambian sus estados coherentemente. Esto significa que el estado del sistema oscila entre $\left| 0,e \right\rangle$ y $\left| 1,g \right\rangle$ , donde $\left| m,g \right\rangle$ representa el estado de la mecánica y del cúbit. Entre un intercambio completo, el cúbit y los osciladores mecánicos están entrelazados con función de estado $\left| 1,g \right\rangle + \left| 0,e \right\rangle$ .

Este intercambio puede ser usado como un método de preparación de estados mecánicos. Los autores primero sintonizan el cúbit para que no esté en resonancia con ninguno de los osciladores mecánicos. Luego, con el modo mecánico vacío de quanta, el cúbit se inicializa con estados $\left| 0,g \right\rangle, \left| 0,e \right\rangle$ o $\left| 0,g \right\rangle + \left| 0,e \right\rangle$ . El estado $\left| m, q \right\rangle$ describe el número de fonones de un oscilador mecánico concreto, $m = 0, 1, 2$ …, y si el cúbit está en su estado fundamental o excitado $q = g, e$ . La frecuencia del cúbit se sintoniza para que esté en resonancia con alguno de los modos mecánicos durante el tiempo correspondiente a un intercambio completo. Cuando la operación de intercambio es aplicada al estado $\left| 0,g \right\rangle$ , el sistema permanece inalterado dado que ambos subsistemas están en su estado fundamental y no hay energía que intercambiar. Durante el intercambio, el estado $\left| 0,e \right\rangle$ se convierte en $\left| 1,g \right\rangle$ como se muestra en la Figura 1. Cuando el cúbit se inicializa en un estado de superposición, el estado es $\left| 0,g \right\rangle + \left| 0,e \right\rangle$ . La operación de intercambio actúa sobre ambas partes de esta superposición dando lugar al estado final $\left| 0,g \right\rangle + \left| 1,g \right\rangle$ . El oscilador mecánico está ahora en un estado de superposición, pero el estado del oscilador mecánico no está entrelazado con el estado del cúbit.

Midiendo un estado mecánico
En el segundo modo de operación, el cúbit no está en resonancia con ninguno de los osciladores, lo cual se conoce como interacción dispersiva. La tasa de interacción dispersiva entre el cúbit y el oscilador mecánico, $\chi$ , se determina ahora por el acoplamiento capacitivo directo, $g$ , la desintonización entre el cúbit y la mecánica, $\Delta$ , y otros parámetros del cúbit. En el límite en que la desintonización entre el cúbit y la mecánica es mayor que la tasa de interacción capacitiva ( $\Delta \gg g$ ), la interacción mostrada en la Ecuación 1 es aproximada por el hamiltoniano fuera de resonancia:

$\mathcal{H}_{\mathrm{off}} = \chi a^{\dagger} a \sigma_z$
[Ecuación 2].

La combinación $a^{\dagger}a$ es la versión en operadores del número de fonones, $m$ , en el oscilador mecánico. $\sigma_z$ es la versión en operadores del estado del cúbit, bien $\left| g \right\rangle$ o bien $\left| e \right\rangle$ .

Sin la interacción entre el cúbit y la mecánica, el hamiltoniano de sólo el cúbit quedaría $\mathcal{H}_{q} = \omega_q \sigma_z$ , donde $\omega_q$ es la frecuencia de transición del cúbit. Cuando añadimos la interacción fuera de resonancia, el hamiltoniano se puede escribir como $\mathcal{H}_{q} + \mathcal{H}_{\mathrm{off}} = (\omega_q - \chi a^{\dagger}a )\sigma_z$ . Comparando el hamiltoniano combinado con el de sólo el cúbit, vemos que el efecto de la interacción es modificar la frecuencia de transición del cúbit (representado por todo lo anterior a $\sigma_z$ ). Por lo que ahora la frecuencia de transición del cúbit depende del número de fonones en el oscilador mecánico ( $m = a^{\dagger}a$ ). Por cada fonón adicional en el oscilador mecánico, la frecuencia de transición del cúbit cambia $\chi$ .

Esta interacción es crucial para poder caracterizar el estado del oscilador mecánico. Dado que un distinto número de fonones imparte un cambio de frecuencia diferente en el cúbit, el estado mecánico está impreso en la frecuencia del cúbit. Para solventar la probabilidad de distinto número de fonones en los osciladores mecánicos, se realiza una medida interferométrica sobre los cúbits. El oscilador mecánico se prepara en un estado de Fock con 0 o 1 fonones o en una superposición de varios fonones 0, 1, 2… Luego, el cúbit se coloca en un estado de superposición $\left| g \right\rangle + \left| e \right\rangle$ y se deja precesar por un tiempo variable, $t$ . Durante este tiempo, el estado superpuesto acumula una fase de $\chi$ si hay un fonón, $2\chi$ para dos fonones y así sucesivamente. La fase acumulada refleja la probabilidad ( $A_n$ ) de que el oscilador mecánico contenga cero, uno, dos, etc. fonones. El estado del cúbit evoluciona a $\left| g \right\rangle + e^{i\phi} \left| e \right\rangle$ , donde la fase acumulada es $\phi = \sum_n A_n n \chi t$ . Los autores rotan el cúbit de vuelta a su base de medición y monitorizan la población final del estado excitado como función del tiempo de interacción, $t$ , y ajustan la trayectoria a la forma funcional

$S(t) = \sum_n A_n e^{-\kappa t/2} \cos [(2 n \chi t) + \phi_n]$
[Ecuación 3]

Esta función incluye las probabilidades del número de fonones, $A_n$ , así como la precesión dependiente de este número $n \chi$ . También incluye el desfase dependiente del número, $\phi_n$ y la constante de decaimiento de fonones, $\kappa$ . Esto captura la dinámica de la trayectoria del cúbit incluso cuando las probabilidades de los fonones van cambiando debido al decaimiento de la energía. La figura a continuación muestra una traza de interferometría y el ajuste que se usó para extraer la población de fonones en el oscilador mecánico. La traza contiene una combinación de varias oscilaciones de frecuencia, cada una de ellas correspondiente a un número de fonones distinto. El peso de una frecuencia particular en la combinación representa la probabilidad de que el correspondiente número de fonones esté presente en el estado mecánico que se vaya a medir.

Figura 3. **Caracterización del estado mecánico.** La interferometría de cúbits se realiza en presencia de fonones en el oscilador mecánico. La trayectoria resultante del estado del cúbit contiene información sobre la distribución de probabilidad del número de fonones. Una traza típica se muestra aquí y se ajusta a la forma funcional de la Ecuación 3 para determinar el índice de fonones del estado mecánico. Figura adaptada de [1].

Entrelazando dos osciladores mecánicos
Con la habilidad de controlar y medir el estado de cada oscilador mecánico, el siguiente paso es preparar un estado del sistema donde el movimiento de los dos osciladores esté entrelazado. Escribimos el estado del cúbit y los dos osciladores como $\left| m_1, q, m_2 \right\rangle$ , donde el oscilador mecánico contiene $m_1, m_2=0,1,2,..$ fonones y el cúbit puede estar tanto en el estado fundamental ( $g$ ) como en el excitado ( $e$ ). Primero, se prepara el cúbit en su estado excitado con $\left| 0,e,0 \right\rangle$ . Medio intercambio entre el cúbit y el primer oscilador mecánico los entrelaza, $\left| 1, g, 0 \right\rangle + \left| 0, e, 0 \right\rangle$ . Esto se consigue llevando el cúbit a resonancia con el oscilador mecánico sólo durante la mitad del tiempo requerido para llevar a cabo un intercambio completo, como se puede ver en la Figura 2. Finalmente, el estado del cúbit se intercambia por completo con el del segundo oscilador mecánico, resultando en el estado $\left| 1, g, 0 \right\rangle + \left| 0, g, 1 \right\rangle$ . Esto deja al cúbit en su estado fundamental con los dos osciladores mecánicos completamente entrelazados entre sí $(\left| 1,0 \right\rangle + \left| 0,1 \right\rangle) \bigotimes \left| g \right\rangle$ .

Perspectiva de futuro
Los autores construyen un dispositivo que acopla el movimiento mecánico a un cúbit superconductor. El cúbit es usado para preparar y medir los modos de un modo mecánico individual. Los autores presentan un protocolo que prepara dos modos mecánicos, ambos acoplados al mismo cúbit, en un estado entrelazado. Este trabajo demuestra los cimientos que se necesitan para construir un sistema cuántico híbrido combinando dos sistemas cuánticos dispares. Los autores emparejan el control preciso del cúbit superconductor con las largas vidas medias de los modos mecánicos para construir un dispositivo que aproveche los puntos fuertes de ambos sistemas. Este tipo de diseño permitirá futuros avances en la computación cuántica, la detección y la comunicación partiendo de muchas tecnologías diferentes.

Referencias

[1] Wollack, E.A., Cleland, A.Y., Gruenke, R.G. et al. Quantum state preparation and tomography of entangled mechanical resonators. Nature 604, 463–467 (2022).

Akash Dixit construye cúbits superconductores y los acopla a cavidades 3D para desarrollar novedosas arquitecturas cuánticas y buscar materia oscura.

Gracias a Joe Kitzman por sus grandes aportaciones y comentarios a la hora de editar este artículo.

Quantum routing with teleportation

This post was sponsored by Tabor Electronics. To keep up to date with Tabor products and applications, join their community on LinkedIn and sign up for their newsletter.

Authors: Dhruv Devulapalli, Eddie Schoute, Aniruddha Bapat, Andrew M. Childs, Alexey V. Gorshkov

arXiv: https://arxiv.org/abs/2204.04185

Background and motivation

When we write quantum circuits on paper or in software, it’s often convenient to assume that any pair of qubits are connected. It’s convenient both (i) as a level of abstraction – we sometimes don’t want to think about low-level hardware details when thinking about algorithms – and (ii) because it’s in some sense true – even if there’s not a direct edge between two qubits, as long as there is some connected path the qubits can interact. This is exhibited in the figure below.

In the left panel, this figure shows a five-qubit superconducting processor from IBMQ, and highlights the qubit connections in the right panel. Qubit Q0 and Q1 are directly connected, but qubit Q0 and Q3 are not. However, there is a connected path from qubit Q0 to Q3, namely the path Q0 – Q2 – Q3. Because there is a connected path, two-qubit operations can be performed between qubits Q0 and Q3.

How is this possible? Swapping two qubits is a unitary operation – indeed a self-inverse operation – and so a permissible quantum operation. Furthermore, it’s safe to assume that this is a readily available operation on a quantum computer. Indeed, we can compose a swap operation out of three controlled-not (CNOT) operations, and CNOTs are commonly assumed to be a primitive operation on a quantum computer. A CNOT is defined as

where a and b are bits and ⊕ denotes addition modulo two. In words, the second qubit is flipped if the first qubit is in the |1⟩ (excited) state. The subscript “12” indicates that qubit 1 is the control and qubit 2 is the target. If we swap this indices, then

From this, a little algebra shows that the composition of three CNOTs implements a swap operation:

So, we can assume we have such a swap operation (SWAP) available between connected qubits.

In the above figure, qubits Q0 and Q3 weren’t directly connected, but they were both connected to qubit Q2. If we swap the state of Q0 and Q2, then there is now a direct connection between Q0 and Q3, and we can perform a two-qubit gate. If we’d like, after the two-qubit gate we can SWAP Q0 and Q2 again to restore the previous configuration. It’s easy to generalize this to any pair of qubits which have a connected path between them. Such a sequence of SWAPs is known as a SWAP network, and the general task of “getting qubits where they need to be” is known as qubit routing. The word “routing” is used in reference to packet switching on networks, for example the internet, a task with many common features.

Thus it’s safe to assume that we can perform a two-qubit gate between any pair of qubits. The downside is the additional SWAP operations needed to do so. Quantum computers are noisy and each operation has some probability of error, so the more operations there are the more likely it is for an error to occur. It is thus of great interest and practical importance to develop procedures to perform qubit routing with the fewest possible resources, i.e., with the shortest possible depth.

Main idea and results of the paper

This paper focuses on performing qubit routing with the fewest possible resources, and in particular considers a clever qubit routing procedure based on teleportation. These authors weren’t the first to consider teleportation for qubit routing, but they analyze it in novel ways. As we will discuss below, teleportation requires local operations (including measurements) and classical communication, abbreviated LOCC. As such, the author’s scheme can be referred to as LOCC routing in general and teleportation routing in particular. Here, we use “TELE routing” to mean teleportation-based routing and “SWAP routing” to mean SWAP-based routing.

The authors’ main strategy is to define metrics for how well qubit routing algorithms perform, then compare TELE routing to SWAP routing in three main categories. What are the three categories? A routing problem is defined by a quantum computer you want to run on and a circuit you want to run. More abstractly, we represent a quantum computer by a graph G where nodes (vertices) are qubits and edges are connections between qubits, and we represent a circuit as a permutation π of the graph. (We don’t care about the operations here, only how to route the qubits, so it’s sufficient to represent the circuit as a permutation.) So, a routing problem is defined by a graph G and a permutation π. The three categories the authors consider are:

A specific graph G and a specific permutation π.
A specific graph G and any permutation π.
Any graph G and any permutation π.

The main results in each category, colloquially stated, are:

There exists a graph G with N nodes and a permutation π such that SWAP routing takes depth of order N and TELE routing takes constant depth independent of N.
There exists a graph G with N nodes such that, for any permutation π on G, SWAP routing takes depth log N and TELE routing takes constant depth independent of N.
For any graph G with N nodes and any permutation π on G, the maximum advantage of TELE routing over SWAP routing is of order (N log N)^½.

The remainder of this article is an invitation to understanding these results, starting with a review of teleportation then walking through the simpler results while providing intuition for the others.

Teleportation

Since we are going to use teleportation as a subroutine for qubit routing, let’s quickly (re-)analyze the protocol. The quantum circuit for teleportation is shown below.

This circuit “teleports” an arbitrary quantum state |𝜓⟩ = α|0⟩ + β|1⟩ on the first qubit to the third qubit by means of local operations (both unitary operations and measurements) and classical communication. Concretely, “classical communication” means performing operations conditional on the measurement outcomes (classical information) of the first two qubits. Because sending this classical information cannot be instantaneous, the name “teleportation” is not to be taken in a literal sense.

We can understand the above circuit for teleportation as follows. The Hadamard and CNOT create a Bell state on the last two qubits. (We omit normalization here and throughout.)

After, we measure the top two qubits in the Bell basis, which corresponds to the Bell state preparation circuit in reverse. Before the measurements, one can show with a little algebra that the final state of the three qubits is as follows (again omitting normalization):

Written this way, it’s easy to see how to always obtain the state |𝜓⟩ on the third qubit after measuring the first two qubits:

If we measure |00⟩ (the first term in the above equation), the state of the third qubit is |𝜓⟩
If we measure |01⟩ (the first term in the above equation), the state of the third qubit is X|𝜓⟩. Perform X to obtain |𝜓⟩.
If we measure |10⟩ (the first term in the above equation), the state of the third qubit is Z|𝜓⟩. Perform Z to obtain |𝜓⟩.
If we measure |11⟩ (the first term in the above equation), the state of the third qubit is XZ|𝜓⟩. Perform XZ to obtain |𝜓⟩.

Thus we always obtain |𝜓⟩ on the third qubit. Now that we have one three-qubit “gadget” for teleportation, we can consider chaining several of these gadgets together to teleport a qubit a greater distance. This is illustrated in Figure 1 of the paper:

Notice the very nice property that the depth of this seven-qubit teleportation circuit is the same as the depth of the three-qubit teleportation circuit. Specifically, both circuits have a depth of four. This is different from using SWAP routing in which the SWAPs have to be sequential as shown below.

Here, the depth of the circuit grows with the number of qubits. This observation is key to understanding why and when teleportation-based routing may be advantageous.

Routing time, and bounds

Let rt(G, π) denote the routing time (minimum circuit depth) to perform the permutation π on the graph G. Let rt(G) denote the worst-case routing time taken over all permutations on G.

Note that any SWAP routing procedure can be “mimicked” by a TELE routing procedure which simply substitutes each SWAP operation with a teleportation gadget, using the same (constant) depth. But, it’s possible for TELE routing to be faster. Therefore, the time for TELE routing is at most the time for SWAP routing.

In prior work, it has been shown that SWAP routing on a graph G with N nodes takes O(N) time. Combining this with the previous argument, we also have that TELE routing takes O(N) time.

In summary, so far we have TELE routing time ≤ SWAP routing time = O(N) on a graph G with N nodes.

It’s also possible to show lower bounds. Since swapping two nodes at a distance d requires at least d SWAPs, we have that the SWAP routing time is at least diam(G). (The diameter of a graph G is the maximum shortest-path distance between any pair of nodes.) This is referred to as the “diameter lower bound” in the paper.

The diameter bound doesn’t apply to TELE routing, but it is possible to provide a lower bound for this. Leaving the proof to an unpublished article by the same authors, the authors provide the bound

where c(G) is the vertex expansion of G and, for connected graphs, is between 2 / N and 1. LOCC routing is the most general, so this implies SWAP routing ≥ TELE routing ≥ 2 / c(G) – 1.

TELE routing vs SWAP routing

Define the teleportation advantage adv(G, π) as the ratio of SWAP routing to TELE routing, i.e.

Category 1: A specific graph G and a specific permutation π

The first case the authors consider is shown below.

Here we have G as a line graph (hollow black nodes with black lines as edges) and π as the permutation which swaps the left-most and right-most qubits. If there are N nodes in G, SWAP routing takes depth of order N because each SWAP must be in parallel. However, as we have seen above, the depth of TELE routing is constant in N. Therefore the teleportation advantage adv(G, π) is of order N, a significant advantage!

The second case the authors consider is similar, shown below.

Here we have the same graph G but a “rainbow permutation” π, so-called because the red lines form a rainbow as drawn above. The parameter 0 < α < 1 quantifies how many nodes appear in the rainbow permutation. By the diameter bound, SWAP routing as depth N. For TELE routing, one can swap each pair of nodes sequentially with a constant depth circuit. Since there are N^α / 2pairs of nodes in the permutation, TELE routing takes depth N^α / 2. So, the teleportation advantage in this case is O(N^{1 – α}). This is sublinear for nonzero α, so less than the linear advantage for the first case, but still advantageous.

One might suppose TELE routing is only advantageous because the diameter of the line graph in the above examples was of order N (the number of nodes). But now consider wrapping the line graph around so two end nodes are connected in a circle. Further, place an additional node in the center of the circle with an edge to every node on the circumference, as shown below.

The diameter of this graph, the so-called “wheel graph” or W_N, is constant, independent of the number of nodes N. (Specifically, the diameter is two.) Now consider the permutation shown in red on this graph. This permutation swaps qubits at a distance l along the “rim” of the wheel. As the authors argue, the SWAP routing time for this case is min(3l, N / l – 1). The 3l corresponds to using the central node to SWAP every pair of qubits sequentially, and the N / l – 1 corresponds to swapping qubits along the rim of the wheel in parallel. Now, for TELE routing, this permutation on G can be done in constant depth by simply teleporting each pair of qubits along the rim in parallel. If we set l to be the square root of N / 2, this yields the maximum teleportation advantage of

Thus, teleportation routing enables super-diametric speedups.

Category 2: A specific graph G and any permutation π

In the above example we got to hand-pick the permutation π. Now let’s consider the more general case of any permutation π, and ask if we can find some graph G where TELE routing is advantageous.

The authors show the answer to this question turns out to be yes: there exists a graph G with N nodes where SWAP routing takes depth at least logarithmic in N, and TELE routing takes constant depth independent of N. The graph G which achieves this is shown below.

This graph has n layers of subgraphs vertically stacked on top of each other. As such, the authors call it L(n). The nth layer is a complete graph on 2ⁿ nodes, shown with blue edges above. These layers are stacked by connecting every node in the current layer to the layer below it, shown with black edges above. For example, the first layer K1 has one node, and an edge to each node in the layer K2 below. The layer K2 has two nodes, and each node is connected to every node in the layer K4 below it. And so on. The total number of nodes in L(n) is 2ⁿ – 1. Imagine building a quantum computer with this topology!

The proofs of the SWAP routing and TELE routing depths quoted above are somewhat involved, so we omit them here and refer the interested reader to the paper (see Sec. V).

Category 3: Any graph G and any permutation π

Last, the authors consider the most general category of any graph G and any permutation π. For this case, the relevant metric is the “maximum teleportation advantage”

The authors prove (Theorem 6.4) that

Thus, for any quantum computer with N qubits, no matter what the topology is or the specific quantum computation we wish to execute, the maximum advantage we can obtain using teleportation-based routing over swap-based routing is of order (N log N)^½. A careful reader may question if this result disagrees with the first example in Category 1 where a specific graph G and specific permutation π admitted a teleportation advantage of order N. There is, however, no disagreement: the present result considers the ratio of worst-case permutations, but the result in Category 1 considers a specific permutation.

While it’s theoretically interesting to consider any graphs G, there are common patterns to which quantum computers are currently built based on engineering and other considerations. For example, superconducting qubits are often arranged in a two-dimensional plane with nearest-neighbor connectivity. The authors specialize the above result to this case of planar graphs and show that there is at most a constant factor advantage to using TELE routing. We remark again that this result considers the ratio of worst-case permutations and does not disagree with previous results concerning specific permutations. Indeed, you may construct or encounter a quantum circuit you wish to run on a planar quantum computer for which teleportation-based routing is significantly more practical, even as a constant factor improvement.

Summary and conclusions

The qubit routing problem is well-motivated by practical considerations and interesting to study. A swap-based routing approach is always possible and bears similarity to similar classical problems. However, just as there are clever, uniquely quantum strategies for subroutines like addition on a quantum computer, there is a clever, uniquely quantum strategy to qubit routing based on teleportation. It’s easy to construct examples where teleportation-based routing is advantageous, and the authors provide general statements about its performance relative to swap-based routing. Although in the most general sense the advantage is at most (N log N)^½for a quantum computer with N qubits – and even at most constant for planar graphs – there are very likely practical scenarios in which teleportation-based routing is likely to be advantageous. So, next time you are pondering practicalities of how an algorithm may run on a quantum computer, keep teleportation as a strategy for qubit routing in the back of your head!

Background and Motivation

Fluxonium Qubits

Adding a tunable coupler…

Time for Quantum Gates

Experimental Results

Conclusion

References

Contexto y motivación

Idea principal y resultados del paper

Teleportación

Tiempo de enrutación y cotas

TELE routing vs SWAP routing

Categoría 1: un grafo G específico y una permutación específica π

Categoría 2: un grafo G específico y cualquier permutación π

Categoría 3: cualquier grafo G y cualquier permutación π

Resumen y conclusiones

Introduction

How they did it

Quantum Protocol

In Summary

References

Introduction:

Experimental Setup and Operating Principle:

Conclusions:

Introducción

Detalles Experimentales

Tasas de Decaimiento del Cúbit

Dinámica y Emisión de un Cúbit Controlado

La Ecuación Maestra de Lindblad

Resultados experimentales

Conclusión

Referencias

A general canonical principle

What if the state of is not the identity?

Background and motivation

Main idea and results of the paper

Teleportation

Routing time, and bounds

TELE routing vs SWAP routing

Category 1: A specific graph G and a specific permutation π

Category 2: A specific graph G and any permutation π

Category 3: Any graph G and any permutation π

Summary and conclusions

***TELE routing* vs *SWAP routing***

What if the state of $R$ is not the identity?